题目内容
【题目】已知函数![]() .
.
(1)当![]() 时,求
时,求![]() 的单调区间;
的单调区间;
(2)若函数![]() 在
在![]() 上无零点,求
上无零点,求![]() 最小值.
最小值.
【答案】(1) ![]() 的单调减区为
的单调减区为![]() ,单调增区间为
,单调增区间为![]() ,(2)
,(2) ![]() 的最小值为
的最小值为![]() .
.
【解析】试题解析: (I)代入a的值,写出函数的解析式,对函数求导,使得导函数大于0,求出自变量的值,写出单调区间.
(II)根据函数无零点,得到函数的导函数小于0在一个区间上不恒成立,得到函数在这个区间上没有零点,构造新函数,对函数求导,利用求最值得方法求出函数的最小值.
(1)当![]() 时,
时,![]() ,
,
则![]() ,由
,由![]() ,得
,得![]() ,由
,由![]() ,得
,得![]() ,
,
故![]() 的单调减区为
的单调减区为![]() ,单调增区间为
,单调增区间为![]() .
.
(2)因为![]() 在区间
在区间![]() 上恒成立不可能,
上恒成立不可能,
故要使函数![]() 在
在![]() 上无零点,只要对任意的
上无零点,只要对任意的![]() ,
,![]() 恒成立,即对
恒成立,即对![]() 恒成立,令
恒成立,令![]() ,则
,则![]() ,再令
,再令![]() ,则
,则![]() ,故
,故![]() 在
在![]() 上为减函数,于是
上为减函数,于是![]() ,从而
,从而![]() ,于是
,于是![]() 在
在![]() 上为增函数,所以
上为增函数,所以![]() ,故要使
,故要使![]() 恒成立,只要
恒成立,只要![]() ,综上,若函数
,综上,若函数![]() 在
在![]() 上无零点,则
上无零点,则![]() 的最小值为
的最小值为![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
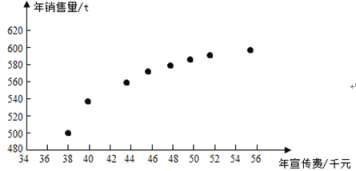
【题目】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费![]() (单位:千元)对年销售量y(单位:t)和年利润z(单位:千元)的影响,对近8年的年宣传费
(单位:千元)对年销售量y(单位:t)和年利润z(单位:千元)的影响,对近8年的年宣传费![]() 和年销售量
和年销售量![]() (
(![]() )数据作了初步处理,得到下面的散点图及一些统计量的值.
)数据作了初步处理,得到下面的散点图及一些统计量的值.
|
|
|
|
|
|
|
46.6 | 563 | 6.8 | 289.8 | 1.6 | 1.469 | 108.8 |
表中![]() ,
,![]()
(1)根据散点图判断,![]() 与
与![]() 哪一个适宜作为年销售量y关于年宣传费x的回归方程类型?给出判断即可,不必说明理由
哪一个适宜作为年销售量y关于年宣传费x的回归方程类型?给出判断即可,不必说明理由
(2)根据(1)的判断结果及表中数据,建立y关于x的回归方程;
(3)已知这种产品的年利润z与x、y的关系为![]() 根据(2)的结果回答下列问题:
根据(2)的结果回答下列问题:
①年宣传费![]() 时,年销售量及年利润的预报值是多少?
时,年销售量及年利润的预报值是多少?
②年宣传费x为何值时,年利润的预报值最大?
附:对于一组数据![]() ,其回归线
,其回归线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: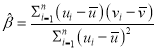 ,
,![]() .
.
