题目内容
【题目】如图,已知正方形OABC边长为3,点M,N分别为线段BC,AB上一点,且2BM=MC,AN=NB,P为△BNM内一点(含边界),设 ![]() (λ,μ为实数),则
(λ,μ为实数),则 ![]() 的最大值为
的最大值为 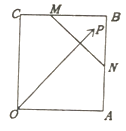
【答案】![]()
【解析】解:如图,以OA为x轴,以OC为y轴,建立直角坐标系,则O(0,0),A(3,0),C(0.3),B(3,3),
∵2BM=MC,AN=NB,
∴M(1,3),N(3, ![]() ),
),
设P(x,y),
∵ ![]() (λ,μ为实数),
(λ,μ为实数),
∴ ![]() =λ(3,0)+μ(0,3)=(3λ,3μ),
=λ(3,0)+μ(0,3)=(3λ,3μ),
∴ ![]() ,即
,即 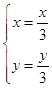 ,
,
∴λ ![]() =
= ![]() ﹣
﹣ ![]() =
= ![]() (3x﹣y),
(3x﹣y),
令z=3x﹣y,即y=3x﹣z,
由M(1,3),N(3, ![]() ),得到直线MN的方程为3x+4x﹣15=0,
),得到直线MN的方程为3x+4x﹣15=0,
则x,y满足的区域为 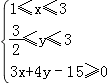 ,如图所示,
,如图所示,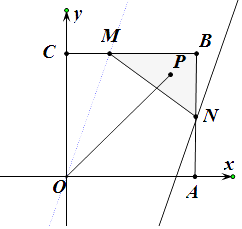
当目标函数z=3x﹣y,过点N(3, ![]() )时,Z最大,
)时,Z最大,
则zmax=3×3﹣ ![]() =9﹣
=9﹣ ![]() =
= ![]() ,
,
∴(λ ![]() )max=
)max= ![]() ×
× ![]() =
= ![]()
所以答案是: ![]()

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目