题目内容
【题目】已知直线l的方程为y=x+2,点P是抛物线y2=4x上到直线l距离最小的点,点A是抛物线上异于点P的点,直线AP与直线l交于点Q,过点Q与x轴平行的直线与抛物线y2=4x交于点B.
(Ⅰ)求点P的坐标;
(Ⅱ)证明直线AB恒过定点,并求这个定点的坐标.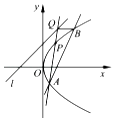
【答案】解:(Ⅰ)设点P的坐标为(x0 , y0),则 ![]() ,
,
所以,点P到直线l的距离  .
.
当且仅当y0=2时等号成立,此时P点坐标为(1,2).
(Ⅱ)设点A的坐标为 ![]() ,显然y1≠2.
,显然y1≠2.
当y1=﹣2时,A点坐标为(1,﹣2),直线AP的方程为x=1;
当y1≠﹣2时,直线AP的方程为  ,
,
化简得4x﹣(y1+2)y+2y1=0;
综上,直线AP的方程为4x﹣(y1+2)y+2y1=0.
与直线l的方程y=x+2联立,可得点Q的纵坐标为 ![]() .
.
因为,BQ∥x轴,所以B点的纵坐标为 ![]() .
.
因此,B点的坐标为  .
.
当 ![]() ,即
,即 ![]() 时,直线AB的斜率
时,直线AB的斜率  .
.
所以直线AB的方程为  ,
,
整理得 ![]() .
.
当x=2,y=2时,上式对任意y1恒成立,
此时,直线AB恒过定点(2,2),
当 ![]() 时,直线AB的方程为x=2,仍过定点(2,2),
时,直线AB的方程为x=2,仍过定点(2,2),
故符合题意的直线AB恒过定点(2,2)
【解析】(Ⅰ)利用点到直线的距离公式,求出最小值,然后求点P的坐标;(Ⅱ)设点A的坐标为 ![]() ,显然y1≠2.通过当y1=﹣2时,求出直线AP的方程为x=1;当y1≠﹣2时,求出直线AP的方程,然后求出Q的坐标,求出B点的坐标,解出直线AB的斜率,推出AB的方程,判断直线AB恒过定点推出结果.
,显然y1≠2.通过当y1=﹣2时,求出直线AP的方程为x=1;当y1≠﹣2时,求出直线AP的方程,然后求出Q的坐标,求出B点的坐标,解出直线AB的斜率,推出AB的方程,判断直线AB恒过定点推出结果.

 阅读快车系列答案
阅读快车系列答案【题目】已知椭圆C1 , 抛物线C2焦点均在x轴上,C1的中心和C2顶点均为原点O,从每条曲线上各取两个点,将其坐标记录于表中,则C1的左焦点到C2的准线之间的距离为( )
x | 3 | ﹣2 | 4 |
|
y | -2 | 0 | ﹣4 |
|
A.![]() -1
-1
B.![]() -1
-1
C.1
D.2