题目内容
【题目】上海市松江区天马山上的“护珠塔”因其倾斜度超过意大利的比萨斜塔而号称“世界第一斜塔”.兴趣小组同学实施如下方案来测量塔的倾斜度和塔高:如图,记O点为塔基、P点为塔尖、点P在地面上的射影为点H.在塔身OP射影所在直线上选点A,使仰角k∠HAP=45°,过O点与OA成120°的地面上选B点,使仰角∠HPB=45°(点A,B,O都在同一水平面上),此时测得∠OAB=27°,A与B之间距离为33.6米.试求: 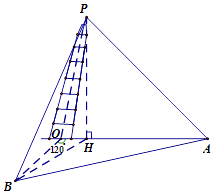
(1)塔高(即线段PH的长,精确到0.1米);
(2)塔身的倾斜度(即PO与PH的夹角,精确到0.1°).
【答案】
(1)解:设塔高PH=x,由题意知,∠HAP=45°,∠HBP=45°,
∴△PAH,△PBH均为等腰直角三角形,
∴AH=BH=x
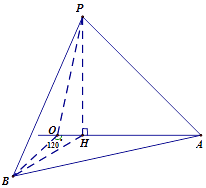
在△AHB中,AH=BH=x,∠HAB=27°,AB=33.6,
∴x= ![]() =
= ![]() =18.86
=18.86
(2)解:在△BOH中,∠BOH=120°,
∴∠OBH=180°﹣120°﹣2×27°=6°,BH=18.86,
由 ![]() =
= ![]() ,
,
得OH= ![]() =2.28,
=2.28,
∴∠OPH=arctan ![]() =arctan
=arctan ![]() =6.89°,
=6.89°,
∴塔高18.9米,塔的倾斜度为6.8°
【解析】(1)由题意可知:△PAH,△PBH均为等腰直角三角形,AH=BH=x,∠HAB=27°,AB=33.6,即可求得x= ![]() =
= ![]() =18.86;(2)∠OBH=180°﹣120°﹣2×27°=6°,BH=18.86,由正弦定理可知:
=18.86;(2)∠OBH=180°﹣120°﹣2×27°=6°,BH=18.86,由正弦定理可知: ![]() =
= ![]() ,OH=
,OH= ![]() =2.28,则倾斜角∠OPH=arctan
=2.28,则倾斜角∠OPH=arctan ![]() =arctan
=arctan ![]() =6.89°.
=6.89°.
【考点精析】解答此题的关键在于理解异面直线及其所成的角的相关知识,掌握异面直线所成角的求法:1、平移法:在异面直线中的一条直线中选择一特殊点,作另一条的平行线;2、补形法:把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体、长方体等,其目的在于容易发现两条异面直线间的关系.

【题目】已知椭圆C1 , 抛物线C2焦点均在x轴上,C1的中心和C2顶点均为原点O,从每条曲线上各取两个点,将其坐标记录于表中,则C1的左焦点到C2的准线之间的距离为( )
x | 3 | ﹣2 | 4 |
|
y | -2 | 0 | ﹣4 |
|
A.![]() -1
-1
B.![]() -1
-1
C.1
D.2