题目内容
【题目】以平面直角坐标系的原点为极点,x轴的正半轴为极轴建立极坐标系.
(1)试分别将曲线C1的极坐标方程ρ=sinθ-cosθ和曲线C2的参数方程![]() (t为参数)化为直角坐标方程和普通方程;
(t为参数)化为直角坐标方程和普通方程;
(2)若红蚂蚁和黑蚂蚁分别在曲线C1和曲线C2上爬行,求红蚂蚁和黑蚂蚁之间的最大距离(视蚂蚁为点).
【答案】(1)C1的直角坐标方程为x2+y2+x-y=0;曲线C2:x2+y2=2(2)![]() .
.
【解析】
(1)将曲线![]() 方程两边同乘以
方程两边同乘以![]() 进行化简;将曲线C2的参数方程分别对
进行化简;将曲线C2的参数方程分别对![]() 进行平方再化简;
进行平方再化简;
(2)由(1)知两个曲线是圆,且内切,故最大距离为大圆的直径.
(1)由题意可得曲线C1的直角坐标方程为
x2+y2+x-y=0,
曲线C2: 即x2+y2=2.
即x2+y2=2.
(2)由(1)知曲线C1、曲线C2均为圆,
圆心分别为![]() 、(0,0),半径分别为
、(0,0),半径分别为![]() ,
,![]() ,
,
则两圆的圆心距为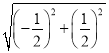 =
=![]() =
=![]()
所以圆C1:x2+y2+x-y=0与圆C2:x2+y2=2内切.
所以红蚂蚁和黑蚂蚁之间的最大距离为圆C2的直径2![]() .
.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目