Question

【题目】在极坐标系中，曲线C1，C2的极坐标方程分别为ρ＝－2cosθ，ρcos＝1.

（1）求曲线C1和C2的公共点的个数；

（2）过极点作动直线与曲线C2相交于点Q，在OQ上取一点P，使|OP|·|OQ|＝2，求点P的轨迹，并指出轨迹是什么图形.

Answer 1

【答案】（1）0；（2）2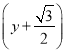＋2＝1；圆.

【解析】

（1）将两个曲线化为普通方程，根据圆心到直线的距离与半径大小进行判定；

（2）用相关点法求解动点的轨迹，利用极坐标进行处理.

（1）C1的直角坐标方程为（x＋1）2＋y2＝1，

它表示圆心为（－1，0），半径为1的圆，

C2的直角坐标方程为x－y－2＝0，

所以曲线C2为直线，

由于圆心到直线的距离为d＝>1，

所以直线与圆相离，即曲线C1和C2没有公共点.

（2）设Q（ρ0，θ0），P（ρ，θ），

则即①

因为点Q（ρ0，θ0）在曲线C2上，

所以ρ0cos＝1，②

将①代入②，得

即为点P的轨迹方程，

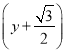化为直角坐标方程为2＋2＝1，

因此点P的轨迹是以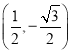为圆心，1为半径的圆.