题目内容
在平面直角坐标系xoy中,已知椭圆C: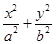 =1(a>b≥1)的离心率e=
=1(a>b≥1)的离心率e= ,且椭圆C上的点到点Q (0,3)的距离最大值为4,过点M(3,0)的直线交椭圆C于点A、B.
,且椭圆C上的点到点Q (0,3)的距离最大值为4,过点M(3,0)的直线交椭圆C于点A、B.
(1)求椭圆C的方程。
(2)设P为椭圆上一点,且满足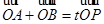 (O为坐标原点),当|AB|<
(O为坐标原点),当|AB|<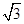 时,求实数t的取值范围.
时,求实数t的取值范围.
(1)  ;(2)
;(2) 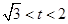 或
或
解析试题分析:(1)此问主要考察椭圆与双曲线的性质,椭圆的离心率与双曲线的性质相等,则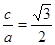 ,利用直线与圆相切得到圆心到直线的距离等于半径,解出
,利用直线与圆相切得到圆心到直线的距离等于半径,解出 ,然后利用
,然后利用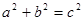 ,解出
,解出 ,得到方程;
,得到方程;
(2)典型的直线与圆锥曲线相交问题,首先方程联立 ,写出根与系数的关系,代入向量相等的坐标表示,得出
,写出根与系数的关系,代入向量相等的坐标表示,得出 点坐标,利用点
点坐标,利用点 在椭圆上,代入方程,然后利用
在椭圆上,代入方程,然后利用 ,利用弦长公式,得到
,利用弦长公式,得到 的范围,与之前得到的
的范围,与之前得到的 与
与 的关系式,求出
的关系式,求出 的范围.
的范围.
试题解析:(1)∵ ∴
∴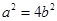 1分
1分
则椭圆方程为 即
即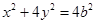 ?设
?设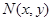 则
则
 ,当
,当 时,
时,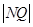 有最大值为
有最大值为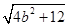 ? 解得
? 解得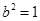 ?∴
?∴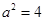 ,椭圆方程是
,椭圆方程是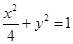 5分
5分
(2)设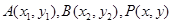 ?
? 方程为
方程为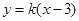 ?
?
由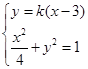 ?整理得
?整理得 .
.
由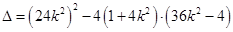
 ,解得
,解得 .
.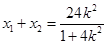 ,
, 7分
7分
∴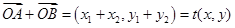 则
则 ,
,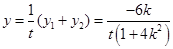 , 由点P在椭圆上,代入椭圆方程得
, 由点P在椭圆上,代入椭圆方程得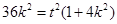 ① 9分
① 9分
又由 ,即
,即 ,
,
将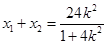 ,
, ,代入得
,代入得 则
则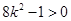 ,
, 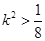 , ∴
, ∴ ② 11分,
② 11分,
由①,得.联立②,解得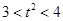
∴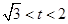 或
或 13分
13分
考点:1.圆锥曲线的性质;2.直线与圆锥曲线相交问题

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
 曲线的一个焦点,并与
曲线的一个焦点,并与 ,求抛物线的方程和双曲线的方程.
,求抛物线的方程和双曲线的方程.  ,过点
,过点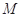
 作直线与抛物线交于两点
作直线与抛物线交于两点 ,
,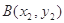 ,过
,过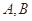 分别作抛物线的切线,两切线的交点为
分别作抛物线的切线,两切线的交点为 .
.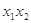 的值;
的值;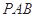 面积的最小值.
面积的最小值.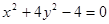 交于A、B两点,记△AOB的面积为S(O是坐标原点).
交于A、B两点,记△AOB的面积为S(O是坐标原点).
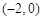 ,
,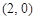 ,并且经过点
,并且经过点 ,求它的标准方程.
,求它的标准方程. 中,以
中,以 为极点,
为极点, 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线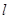 的极坐标方程为
的极坐标方程为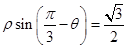 ,曲线
,曲线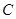 的参数方程为
的参数方程为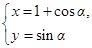 (
(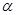 为参数,
为参数,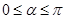 ).
). ·
· =0,设P为弦AB的中点.
=0,设P为弦AB的中点.
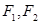 分别是椭圆
分别是椭圆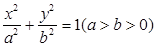 的左右焦点,
的左右焦点,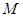 是
是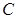 上一点且
上一点且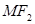 与
与 轴垂直,直线
轴垂直,直线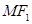 与
与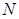 .
.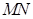 的斜率为
的斜率为 ,求
,求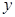 轴上的截距为
轴上的截距为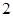 ,且
,且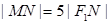 ,求
,求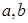 .
.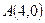
 和
和 ,
,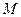 是椭圆
是椭圆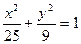 上一动点,则
上一动点,则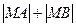 的最大值是____________
的最大值是____________