题目内容
如图所示,现有一边长为6的正方形铁板,如果从铁板的四个角各截出去一个相同的小正方形,做成一个长方体形的无盖容器为使其容积最大,截下的小正方形边长应为多少?

当截下的正方形边长为1时,容积最大.
本题是考察导数应用的题目先设截下的小正方形边长x,然后建立容积V(x)的关系式,再求导,根据导数等于零,确定最值一般地在应用题中,一般考察的都是单峰函数,导数等于零的位置只有一个,它就是要求的最值位置
解:设截下的小正方形边长x,容器容积为
V(x),则做成长方体形无盖容器底面边长
为8-2x,高为X,于是
V(x)=(6-2x)2 x,0<x<3
即 V(x)=4x3 -24x2+36x,0<x<3
有 V'(x)=12x2-48x+36
令V'(x)=0,即令12x2-48x+36=0
解得x1=1,x2=3(舍去)
当0<x<1时,V'(x)>0;当1<x<3时,V'(x)<0
因此x=1是极大值点,且在区间(1,3)内,是唯一的极值点,所以x=1是V(x)的最大值点
即当截下的正方形边长为1时,容积最大
解:设截下的小正方形边长x,容器容积为
V(x),则做成长方体形无盖容器底面边长
为8-2x,高为X,于是
V(x)=(6-2x)2 x,0<x<3
即 V(x)=4x3 -24x2+36x,0<x<3
有 V'(x)=12x2-48x+36
令V'(x)=0,即令12x2-48x+36=0
解得x1=1,x2=3(舍去)
当0<x<1时,V'(x)>0;当1<x<3时,V'(x)<0
因此x=1是极大值点,且在区间(1,3)内,是唯一的极值点,所以x=1是V(x)的最大值点
即当截下的正方形边长为1时,容积最大

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
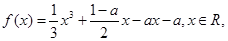 其中a>0.
其中a>0.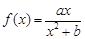 在
在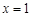 处取得极值2.
处取得极值2.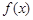 的解析式;
的解析式;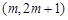 上是单调函数,求实数m的取值范围;
上是单调函数,求实数m的取值范围;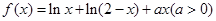 .
.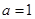 时,求
时,求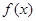 的单调区间;
的单调区间;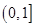 上的最大值为
上的最大值为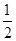 ,求
,求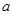 的值.
的值.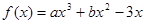 在
在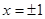 处取得极值,过点
处取得极值,过点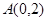 作曲线
作曲线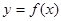 的切线
的切线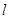 ,(1)求此切线
,(1)求此切线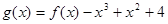 的图象围成的平面图形的面积。
的图象围成的平面图形的面积。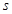 (单位:m)关于时间
(单位:m)关于时间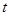 (单位:s)的函数为
(单位:s)的函数为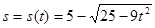 ,求当
,求当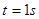 时,梯子上端下滑的速度为( )
时,梯子上端下滑的速度为( )



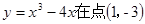 处的切线倾斜角为________.
处的切线倾斜角为________. ,则
,则 = ( )
= ( )


