题目内容
(本小题满分14分)
设椭圆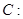
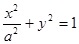 (
(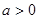 )的两个焦点是
)的两个焦点是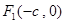 和
和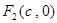 (
(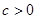 ),且椭圆
),且椭圆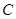 与圆
与圆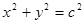 有公共点.
有公共点.
(1)求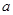 的取值范围;
的取值范围;
(2)若椭圆上的点到焦点的最短距离为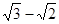 ,求椭圆的方程;
,求椭圆的方程;
(3)对(2)中的椭圆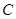 ,直线
,直线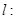
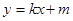 (
(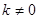 )与
)与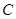 交于不同的两点
交于不同的两点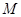 、
、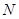 ,若线段
,若线段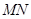 的垂直平分线恒过点
的垂直平分线恒过点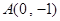 ,求实数
,求实数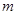 的取值范围.
的取值范围.
(1)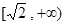 (2)
(2)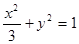 (3)
(3)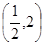
解析试题分析:解:(1)由已知,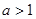 ,
,
∴方程组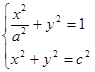 有实数解,从而
有实数解,从而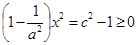 ,故
,故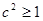 …2分
…2分
所以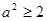 ,即
,即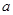 的取值范围是
的取值范围是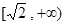 . ……………4分
. ……………4分
(2)设椭圆上的点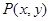 到一个焦点
到一个焦点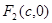 的距离为
的距离为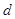 ,
,
则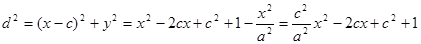
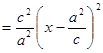 (
(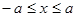 ). ……………6分
). ……………6分
∵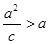 ,∴当
,∴当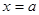 时,
时,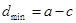 ,
,
于是,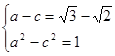 ,解得
,解得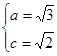 .
.
∴所求椭圆方程为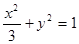 . ……………8分
. ……………8分
(3)由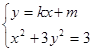 得
得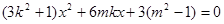 (*)
(*)
∵直线与椭圆交于不同两点, ∴△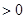 ,即
,即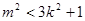 .① ………10分
.① ………10分
设 、
、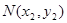 ,则
,则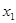 、
、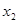 是方程(*)的两个实数解,
是方程(*)的两个实数解,
∴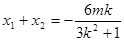 ,∴线段
,∴线段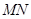 的中点为
的中点为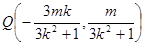 ,
,
又∵线段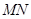 的垂直平分线恒过点
的垂直平分线恒过点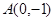 ,∴
,∴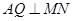 ,
,
即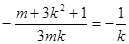 ,即
,即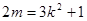 (k
(k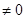 )② ……………12分
)② ……………12分
由①,②得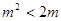 ,
,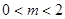 ,又由②得
,又由②得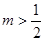 ,
,
∴实数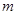 的取值范围是
的取值范围是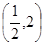 . ……………14分
. ……………14分
考点:椭圆的方程和性质;直线的方程;两直线垂直的判定定理。
点评:本题第一小题也可这样来求解,椭圆跟y轴正半轴的交点为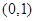 ,若椭圆要与圆
,若椭圆要与圆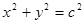 相交,则
相交,则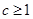 ;第二小题可以结合椭圆的特点来求,当椭圆上的点是
;第二小题可以结合椭圆的特点来求,当椭圆上的点是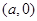 时,它到附近的焦点的距离就是最短距离;第三小题需要注意直线与椭圆相交时应满足的条件。
时,它到附近的焦点的距离就是最短距离;第三小题需要注意直线与椭圆相交时应满足的条件。

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
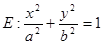 的右焦点
的右焦点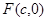 ,且
,且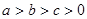 ,设短轴的一个端点为
,设短轴的一个端点为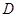 ,原点
,原点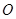 到直线
到直线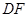 的距离为
的距离为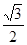 ,过原点和
,过原点和 轴不重合的直线与椭圆
轴不重合的直线与椭圆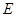 相交于
相交于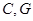 两点,且
两点,且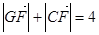 .
.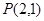 的直线
的直线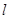 与椭圆
与椭圆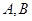 ,且使得
,且使得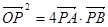 成立?若存在,试求出直线
成立?若存在,试求出直线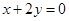 与圆
与圆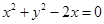 的交点为A、B,
的交点为A、B,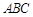 的两个顶点
的两个顶点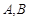 的坐标分别是
的坐标分别是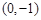 ,
,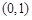 ,且
,且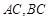 所在直线的斜率之积等于
所在直线的斜率之积等于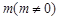 .
.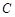 的轨迹
的轨迹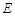 的方程,并判断轨迹
的方程,并判断轨迹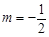 时,过点
时,过点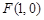 的直线
的直线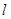 交曲线
交曲线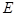 于
于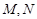 两点,设点
两点,设点 关于
关于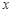 轴的对称点为
轴的对称点为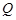 (
(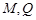 不重合).求证直线
不重合).求证直线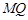 与
与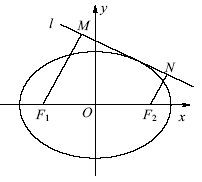
 的方程为
的方程为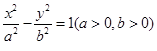 ,
,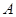 、
、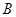 为其左、右两个顶点,
为其左、右两个顶点,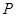 是双曲线
是双曲线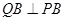 ,
,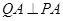 ,垂足分别为
,垂足分别为 与
与 交于点
交于点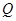 .
.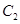 方程;
方程; 、
、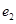 ,当
,当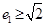 时,求
时,求 的焦点与双曲线
的焦点与双曲线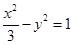 的右焦点重合.
的右焦点重合. ,
, 是抛物线
是抛物线 上相异两点,且满足
上相异两点,且满足 .
. 的中垂线经过点
的中垂线经过点 ,求直线
,求直线 轴于点
轴于点 ,求
,求 的面积的最大值及此时直线
的面积的最大值及此时直线 的顶点在坐标原点,它的准线经过双曲线
的顶点在坐标原点,它的准线经过双曲线 :
: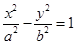 的一个焦点
的一个焦点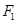 且垂直于
且垂直于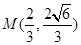 .
.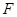 的坐标;
的坐标; .
.