题目内容
【题目】已知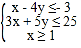
，（本题不作图不得分）
（1）求
的最大值和最小值；
（2）求
的取值范围．
【答案】（1）最大值为12，最小值3； （2）
.
【解析】
（1）由约束条件作出可行域，化目标函数为直线方程的斜截式，数形结合得到最优解，联立方程组求得最优解的坐标，把最优解的坐标代入目标函数得结论；（2）
的几何意义表示区域内的点与
连接直线的斜率，可得与
连接的直线斜率最小，与
连接的直线斜率最大，从而可得结果.
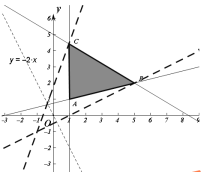
（1）由已知得到平面区域：z=2x+y变形为y=-2x+z，
当此直线经过图中A时使得直线在y轴的截距最小，z最小，
经过图中B时在y轴的截距最大，z 最大，A（1，1），B（5，2），
所以z=2x+y的最大值为2×5+2=12，最小值2×1+1=3；
（2）的几何意义表示区域内的点与（-1，-1）连接直线的斜率，
所以与B连接的直线斜率最小，与C连接的直线斜率最大，
所以的最小值为
，最大值为
所以 的取值范围是．
练习册系列答案
相关题目
【题目】某校高三年级有500名学生，为了了解数学学科的学习情况，现随机抽出若干名学生在一次测试中的数学成绩（满分150分），制成如下频率分布表：
分组 | 频数 | 频率 |
| ① | ② |
| 0.050 | |
| 0.200 | |
| 12 | 0.300 |
| 0.275 | |
| 4 | ③ |
| 0.050 | |
合计 | ④ |
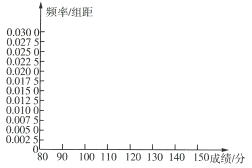
（1）①②③④处应分别填什么？
（2）根据频率分布表完成频率分布直方图.
（3）试估计该校高三年级在这次测试中数学成绩的平均分.
