题目内容
2．设集合P={-1，0，1}，Q={x|$\sqrt{x}$＜$\sqrt{2}$}，则P∩Q=（ ）| A． | {0，1} | B． | {1} | C． | {0} | D． | {-1，0，1} |
分析 求出集合Q，然后求解交集即可．
解答 解：集合P={-1，0，1}，
Q={x|$\sqrt{x}$＜$\sqrt{2}$}={x|0＜x＜2}，
则P∩Q={0，1}．
故选：A．
点评 本题考查集合的基本运算，基本知识的考查．
练习册系列答案
相关题目
16．已知a+2b=2，a＞0，b＞0，则$\frac{1}{2a}$+$\frac{2a}{b}$的最小值是（ ）
| A． | 2 | B． | $\frac{9}{4}$ | C． | $\frac{11}{4}$ | D． | $\frac{9}{2}$ |
14．函数y=2${\;}^{{x}^{2}}$（x∈R）满足（ ）
| A． | 在（-∞，+∞）上是增函数 | |
| B． | 在（-∞，+∞）上是减函数 | |
| C． | 在（-∞，0]上是增函数，在[0，+∞）上是减函数 | |
| D． | 在（-∞，0]上是减函数，在[0，+∞）上是增函数 |
7．设随机变量X服从正态分布N（3，4），则P（X＜1-3a）=P（X＞a2+7）成立的一个必要不充分条件是（ ）
| A． | a=1或2 | B． | a=±1或2 | C． | a=2 | D． | a=$\frac{3-\sqrt{5}}{2}$ |
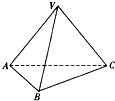如图，三棱锥V-ABC的底面为正三角形，侧面VAC与底面垂直，且VA=VC，已知其侧（左）视图的面积为$\sqrt{3}$，其正（主）视图的面积为2．