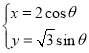题目内容
【题目】已知椭圆
的左右焦点分别为
，
，离心率是
，P为椭圆上的动点.当
取最大值时，
的面积是
（1）求椭圆的方程：
（2）若动直线l与椭圆E交于A，B两点，且恒有
，是否存在一个以原点O为圆心的定圆C，使得动直线l始终与定圆C相切？若存在，求圆C的方程，若不存在，请说明理由
【答案】（1）
；（2）存在，
【解析】
（1）根据余弦定理和基本不等式确定点P为椭圆短轴端点时，
取最大值，再根据三角形面积及
，求得
，
，
，即可得到答案；
（2）对直线的斜率分存在和不存在两种情况讨论，当直线斜率存在时，设直线
的方程为
，
，
，利用向量数量积的坐标运算及韦达定理可得
，即可得到答案；
（1）依题意可得
，
设
，由余弦定理可知：
，
所以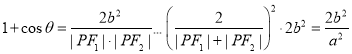
，
当且仅当
（即P为椭圆短轴端点）时等号成立，且取最大值；
此时
的面积是
，
同时，联立
和
解得，，，
所以椭圆方程为.
（2）当直线l斜率不存在时，直线l的方程为
，
所以
，
，此时，
当直线的斜率存在时，设直线的方程为，，，
原点O到直线1的距离为d，所以
，
整理得
，
由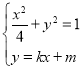
，可得
，
，
，
， 
，恒成立，
即
恒成立 ，
所以
，所以，
所以定圆C的方程是
所以当
时 ， 存在定圆C始终与直线l相切 ，
其方程是.
王后雄学案教材完全解读系列答案
海淀课时新作业金榜卷系列答案
【题目】某企业为确定下一年投入某种产品的研发费用，需了解年研发费用
（单位：千万元）对年销售量
（单位：千万件）的影响，统计了近
年投入的年研发费用
与年销售量
的数据，得到散点图如图所示．
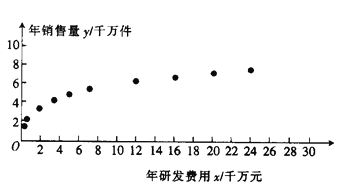
(1)利用散点图判断
和
（其中
均为大于
的常数）哪一个更适合作为年销售量和年研发费用的回归方程类型（只要给出判断即可，不必说明理由）
(2)对数据作出如下处理，令
，得到相关统计量的值如下表：根据第(1)问的判断结果及表中数据，求关于的回归方程；
|
|
|
|
15 | 15 | 28.25 | 56.5 |
(3)已知企业年利润
（单位：千万元）与的关系为
（其中
），根据第(2)问的结果判断，要使得该企业下一年的年利润最大，预计下一年应投入多少研发费用?
附：对于一组数据
，其回归直线
的斜率和截距的最小二乘估计分别为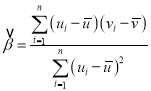
，
