题目内容
1.已知ABCDEF是正六边形,在下列4个表达式(1)$\overrightarrow{FE}$+$\overrightarrow{ED}$,(2)2$\overrightarrow{BC}$+$\overrightarrow{DC}$,(3)$\overrightarrow{BC}$+$\overrightarrow{CD}$+$\overrightarrow{EC}$,(4)2$\overrightarrow{ED}$-$\overrightarrow{FA}$中,运算结果与$\overrightarrow{AC}$相等的表达式共有4个.
分析 根据平面向量的加减运算法则,结合图形,进行化简,即可得出正确的结论.
解答 解:(1)如图1所示,正六边形ABCDEF中,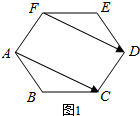
$\overrightarrow{FE}$+$\overrightarrow{ED}$=$\overrightarrow{FD}$=$\overrightarrow{AC}$,
(2)如图2所示,
2$\overrightarrow{BC}$+$\overrightarrow{DC}$=$\overrightarrow{AD}$+$\overrightarrow{DC}$=$\overrightarrow{AC}$,
(3)如图3所示,
$\overrightarrow{BC}$+$\overrightarrow{CD}$+$\overrightarrow{EC}$=$\overrightarrow{BD}$+$\overrightarrow{FB}$=$\overrightarrow{FD}$=$\overrightarrow{AC}$,
(4)如图4所示,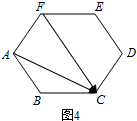
2$\overrightarrow{ED}$-$\overrightarrow{FA}$=$\overrightarrow{FC}$-$\overrightarrow{FA}$=$\overrightarrow{AC}$,
综上,运算结果与$\overrightarrow{AC}$相等的表达式有4个.
故答案为:4.
点评 本题考查了平面向量的应用问题,解题时应画出图形,结合图形进行解答,是基础题目.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16. 如图,设A,B两点在河的两岸,一测量者在点A所在的同侧河岸边选定一点C,测出AC的距离为100m,∠ACB=45°,∠CAB=105°后,就可以计算出A,B两点的距离为( )
如图,设A,B两点在河的两岸,一测量者在点A所在的同侧河岸边选定一点C,测出AC的距离为100m,∠ACB=45°,∠CAB=105°后,就可以计算出A,B两点的距离为( )
 如图,设A,B两点在河的两岸,一测量者在点A所在的同侧河岸边选定一点C,测出AC的距离为100m,∠ACB=45°,∠CAB=105°后,就可以计算出A,B两点的距离为( )
如图,设A,B两点在河的两岸,一测量者在点A所在的同侧河岸边选定一点C,测出AC的距离为100m,∠ACB=45°,∠CAB=105°后,就可以计算出A,B两点的距离为( )| A. | 100$\sqrt{3}$ m | B. | 100$\sqrt{2}$ m | C. | 50$\sqrt{2}$ m | D. | 25$\sqrt{2}$ m |
6.下列命题中为假命题是( )
| A. | $?{x_0}∈R.{log_{\frac{1}{2}}}{x_0}$=-1 | B. | $?x∈R{(\frac{1}{2})^x}$>0 | ||
| C. | ?x∈R x2+2x+3>0 | D. | ?x0∈R.cosx0=-$\frac{{\sqrt{5}}}{2}$ |
11.在△ABC中,a、b、c分别是角A、B、C的对边,如果a,b,c成等差数列,B=60°,△ABC的面积为3$\sqrt{3}$,那么b等于( )
| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |