题目内容
11.在△ABC中,a、b、c分别是角A、B、C的对边,如果a,b,c成等差数列,B=60°,△ABC的面积为3$\sqrt{3}$,那么b等于( )| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
分析 由a、b、c成等差数列,把a+c用b表示,由面积等于3$\sqrt{3}$求出ac=12,结合余弦定理列式求b的值.
解答 解:在△ABC中,∵a、b、c成等差数列,∴2b=a+c,
又∠B=60°,△ABC的面积为3$\sqrt{3}$,
∴$\frac{1}{2}$acsinB=$\frac{1}{2}$acsin60°=3$\sqrt{3}$,即$\frac{1}{2}$×$\frac{\sqrt{3}}{2}$ac=3$\sqrt{3}$,ac=12.
由余弦定理b2=a2+c2-2accosB,得:
b2=a2+c2-2accos60°,即b2=(a+c)2-3ac,
∴b2=4b2-3×12,
∴b=2$\sqrt{3}$.
故选:B.
点评 本题考查了等差数列的性质,考查了三角形的面积公式,训练了余弦定理的应用,属中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.已知5cos2α+4cos2β=4cosα,则2cos2α+cos2β+1的取值范围是( )
| A. | [0,$\frac{16}{25}$] | B. | [-$\frac{5}{2}$,2] | C. | [-$\frac{5}{2}$,$\frac{3}{2}$] | D. | [0,$\frac{32}{25}$] |

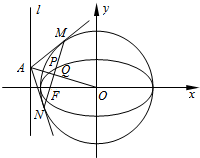 在平面直角坐标系xoy中,设椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左焦点为F,左准线为l.P为椭圆C上任意一点,直线OQ⊥FP,垂足为Q,直线OQ与l交于点A.
在平面直角坐标系xoy中,设椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左焦点为F,左准线为l.P为椭圆C上任意一点,直线OQ⊥FP,垂足为Q,直线OQ与l交于点A.