题目内容
6．李老师从课本上抄录一个随机变量ξ的概率分布列如表：| x | 1 | 2 | 3 |
| P（ξ=x） | ！ | ？ | ！ |
| A． | $\frac{2}{3}$ | B． | 2 | C． | 7 | D． | $\frac{7}{9}$ |
分析 根据概率分布列的概率的和为1，表示“！”都为x，则“？”为1-2x，利用离散型的数学期望的计算方法
求解即可．
解答 解：根据题意设两个“！”都为x，则“？”为1-2x，
根据概率分布列得出数学期望E（ξ）=1•x+2•（1-2x）+3x=2-4x+4x=2，
故选：B
点评 本题考察了概率分布列的概念，离散型的数学期望的计算方法，属于中档题，大胆的表示即可得出答案．
练习册系列答案
相关题目
11．
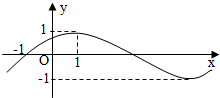已知函数f（x）=Asin（ωx+ϕ），x∈R（其中A＞0，ω＞0，-$\frac{π}{2}$＜ϕ＜$\frac{π}{2}$），其部分图象如下图所示，将f（x）的图象纵坐标不变，横坐标变成原来的$\frac{1}{2}$倍，再向右平移1个单位得到g（x）的图象，则函数g（x）的解析式为（ ）
已知函数f（x）=Asin（ωx+ϕ），x∈R（其中A＞0，ω＞0，-$\frac{π}{2}$＜ϕ＜$\frac{π}{2}$），其部分图象如下图所示，将f（x）的图象纵坐标不变，横坐标变成原来的$\frac{1}{2}$倍，再向右平移1个单位得到g（x）的图象，则函数g（x）的解析式为（ ）| A． | g（x）=sin$\frac{π}{8}$（x+1） | B． | g（x）=sin（$\frac{π}{2}$x-$\frac{π}{4}$） | C． | g（x）=sin（$\frac{π}{8}$x+1） | D． | g（x）=sin（$\frac{π}{2}$x+$\frac{π}{4}$） |
15．某学校有学生2500人，教师350人，后勤职工150人，为了调查对食堂服务的满意度，用分层抽样从中抽取300人，则学生甲被抽到的概率为（ ）
| A． | $\frac{1}{10}$ | B． | $\frac{1}{300}$ | C． | $\frac{1}{2500}$ | D． | $\frac{1}{3000}$ |
16．如图是高中课程结构图：音乐所属课程是（ ）
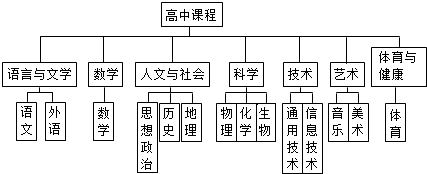
| A． | 艺术 | B． | 人文与社会 | C． | 技术 | D． | 科学 |