题目内容
12.曲线y=5sin(2x+$\frac{π}{6}$)与直线y=x共有7个公共点,与曲线y=log2x共有21个公共点.分析 作曲线y=5sin(2x+$\frac{π}{6}$)与直线y=x的图象,曲线y=5sin(2x+$\frac{π}{6}$)与直线y=log2x的图象;由数形结合求解即可.
解答 解:作曲线y=5sin(2x+$\frac{π}{6}$)与直线y=x的图象如下,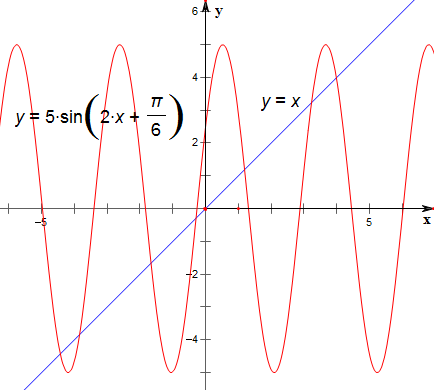
结合图象可得,有7个交点;
作曲线y=5sin(2x+$\frac{π}{6}$)与直线y=log2x的图象如下,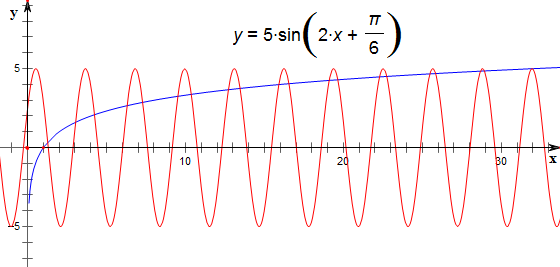
y=5sin(2x+$\frac{π}{6}$)的周期为π,且10π+$\frac{π}{6}$<32;
故结合图象可得,
共有21个交点,
故答案为:7,21.
点评 本题考查了学生作图与识图能力,同时考查了数形结合的思想应用,属于中档题.

练习册系列答案
相关题目
20.sin(θ+75°)+cos(θ+45°)-$\sqrt{3}$cos(θ+15°)=( )
| A. | ±1 | B. | 1 | C. | -1 | D. | 0 |
4.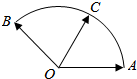 给定两个长度为1的平面向量$\overrightarrow{OA}$和$\overrightarrow{OB}$,它们的夹角为120°如图所示,点C在以O为圆心的圆弧$\overrightarrow{AB}$上变动.若$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,其中x,y∈R,则x+y的最大值是( )
给定两个长度为1的平面向量$\overrightarrow{OA}$和$\overrightarrow{OB}$,它们的夹角为120°如图所示,点C在以O为圆心的圆弧$\overrightarrow{AB}$上变动.若$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,其中x,y∈R,则x+y的最大值是( )
 给定两个长度为1的平面向量$\overrightarrow{OA}$和$\overrightarrow{OB}$,它们的夹角为120°如图所示,点C在以O为圆心的圆弧$\overrightarrow{AB}$上变动.若$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,其中x,y∈R,则x+y的最大值是( )
给定两个长度为1的平面向量$\overrightarrow{OA}$和$\overrightarrow{OB}$,它们的夹角为120°如图所示,点C在以O为圆心的圆弧$\overrightarrow{AB}$上变动.若$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,其中x,y∈R,则x+y的最大值是( )| A. | $\sqrt{2}$ | B. | 2 | C. | $\sqrt{3}$ | D. | 3 |
2.定义$\frac{n}{{p}_{1}+{p}_{2}+…+{p}_{n}}$为n个正数p1,p2,…,pn的“均倒数”.若已知正数数列{an}的前n项的“均倒数”为$\frac{1}{2n+1}$,又bn=$\frac{{a}_{n}+1}{4}$,则$\frac{1}{{b}_{1}{b}_{2}}$+$\frac{1}{{b}_{2}{b}_{3}}$+$\frac{1}{{b}_{3}{b}_{4}}$+…+$\frac{1}{{b}_{2014}{b}_{2015}}$的值为( )
| A. | $\frac{1}{2014}$ | B. | $\frac{1}{2015}$ | C. | $\frac{2013}{2014}$ | D. | $\frac{2014}{2015}$ |