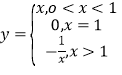题目内容
【题目】已知关于![]() 的一元二次方程
的一元二次方程![]() ,其中
,其中![]() 。
。
(I)若![]() 随机选自集合
随机选自集合![]() ,
,![]() 随机选自集合
随机选自集合![]() ,求方程有实根的概率;
,求方程有实根的概率;
(Ⅱ)若![]() 随机选自区间
随机选自区间![]() ,
,![]() 随机选自区间
随机选自区间![]() ,求方程有实根的概率。
,求方程有实根的概率。
【答案】(I)![]() (Ⅱ)
(Ⅱ)![]()
【解析】
试题分析:先确定关于![]() 的一元二次方程
的一元二次方程![]() 有实根,则满足
有实根,则满足![]() ,而(I)中根据
,而(I)中根据![]() 的取值范围可知,是古典概型,按照古典概型计算概率的方法计算即可;而(Ⅱ)中根据
的取值范围可知,是古典概型,按照古典概型计算概率的方法计算即可;而(Ⅱ)中根据![]() 的取值范围可知,是几何概型,按照几何概型计算概率的方法计算即可
的取值范围可知,是几何概型,按照几何概型计算概率的方法计算即可
试题解析:设“关于![]() 的一元二次方程
的一元二次方程![]() 有实根”为事件
有实根”为事件![]() ,由
,由![]() ,得
,得![]() ,因为
,因为![]() ,所以
,所以![]() 时事件
时事件![]() 发生。
发生。
(I)可能发生的基本事件共20个:(0,0),(0,1),(0,2),(0,3),(1,0),(1,1),(1,2),(1,3)(2,0),(2,1),(2,2),(2,3),(3,0),(3,1),(3,2),(3,3),(4,0),(4,1),(4,2),
(4,3),事件![]() 包含14个基本事件,所以
包含14个基本事件,所以![]() 。
。
(II)因为![]() ,则试验的全部结果构成区域
,则试验的全部结果构成区域![]() ,
,![]() 的面积为
的面积为![]() ,事件
,事件![]() 所构成的区域
所构成的区域![]() ,
,![]() 的面积为
的面积为![]()
![]() ,所以
,所以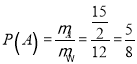

练习册系列答案
相关题目
【题目】市政府为了节约用水,调查了100位居民某年的月均用水量(单位:![]() ),频数分布如下:
),频数分布如下:
分组 |
|
|
|
|
|
|
|
|
|
频数 | 4 | 8 | 15 | 22 | 25 | 14 | 6 | 4 | 2 |

(1)根据所给数据将频率分布直图补充完整(不必说明理由);
(2)根据频率分布直方图估计本市居民月均用水量的中位数;
(3)根据频率分布直方图估计本市居民月均用水量的平均数(同一组数据由该组区间的中点值作为代表).