题目内容
【题目】如图1,在直角梯形ABCD中,AD∥BC,AD⊥DC,BC=2AD=2DC,四边形ABEF是正方形.将正方形ABEF沿AB折起到四边形ABE1F1的位置,使平面ABE1F1⊥平面ABCD,M为AF1的中点,如图2. 
(I)求证:AC⊥BM;
(Ⅱ)求平面CE1M与平面ABE1F1所成锐二面角的余弦值.
【答案】解:(Ⅰ)证明四边形ABE1F1是正方形,∴BE1⊥AB.
平面ABE1F1⊥平面ABCD,平面ABE1F1∩平面ABCD=AB,BE1面ABE1F1
∴BE1⊥平面ABCD,
∵AC平面ABCD,∴BE1⊥AC.
设AD=1,则AC=AB= ![]() ,∴AC⊥AB且AB∩BE1=B.
,∴AC⊥AB且AB∩BE1=B.
∴AC⊥面ABE1F1,又MB面ABE1F1∴AC⊥MB.
(Ⅱ)如图以B为原点,建立如图所示的空间直角坐标系.
则A(1,1,0),B(0,0,0),C(2,0,0),E1(0,0, ![]() ),M(1,1,
),M(1,1, ![]() ).
).
由题意得, 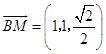 ,
, ![]() ,
, 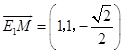 ,
,
设面CE1M的一个法向量为 ![]() ,
,
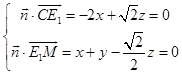 ,可得
,可得 ![]() .
.
又平面ABE1F1得法向量为 ![]() .
.
设平面CE1M与平面ABE1F1所成锐二面角为θ.
cosθ=|cos ![]() |=
|= ![]() .
.
∴平面CE1M与平面ABE1F1所成锐二面角的余弦值为 ![]() .
.
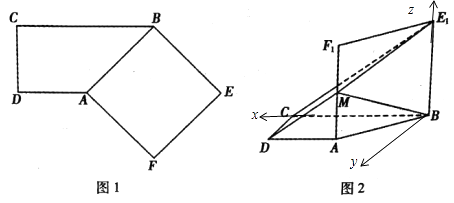
【解析】(Ⅰ)只需证明BE1⊥AC.AC⊥AB且AB,可得AC⊥面ABE1F1,AC⊥MB.(Ⅱ)以B为原点,建立如图所示的空间直角坐标系.则A(1,1,0),B(0,0,0),C(2,0,0),E1(0,0, ![]() ),M(1,1,
),M(1,1, ![]() ).利用向量求解
).利用向量求解
【考点精析】掌握直线与平面垂直的性质是解答本题的根本,需要知道垂直于同一个平面的两条直线平行.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目

