题目内容

【题目】设等差数列{an}的前n项和为Sn ， 若S9=81，a3+a5=14．
（1）求数列{an}的通项公式；
（2）设bn= ，若{bn}的前n项和为Tn ， 证明：Tn＜ ．

【答案】
（1）解：∵{an}等差数列，

由S9=9a5=81，得a5=9．

又由a3+a5=14，得a3=5．

由上可得等差数列{an}的公差d=2．

∴an=a3+（n﹣3）d=2n﹣1．


（2）解：证明：由 ．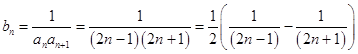

得


【解析】（1）利用等差数列的通项公式性质及其求和公式即可得出．（2）利用裂项求和、数列的单调性即可得出．
【考点精析】利用等差数列的前n项和公式和数列的前n项和对题目进行判断即可得到答案，需要熟知前n项和公式：；数列{an}的前n项和sn与通项an的关系．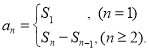

练习册系列答案
相关题目

【题目】甲、乙两人组成“星队”参加猜成语活动，每轮活动由甲、乙各猜一个成语，在一轮活动中，如果两人都猜对，则“星队”得3分；如果只有一个人猜对，则“星队”得1分；如果两人都没猜对，则“星队”得0分．已知甲每轮猜对的概率是 ，乙每轮猜对的概率是 ；每轮活动中甲、乙猜对与否互不影响．各轮结果亦互不影响．假设“星队”参加两轮活动，求：
（1）“星队”至少猜对3个成语的概率；
（2）“星队”两轮得分之和为X的分布列和数学期望EX．

【题目】已知椭圆C： =1（a＞b＞0）过点M（2，1），且离心率为 ． （Ⅰ）求椭圆C的方程；
（Ⅱ）设A（0，﹣1），直线l与椭圆C交于P，Q两点，且|AP|=|AQ|，当△OPQ（O为坐标原点）的面积S最大时，求直线l的方程．

【题目】已知函数 ．

（1）当时，函数恒有意义，求实数的取值范围；

（2）是否存在这样的实数，使得函数f（x）在区间上为减函数，并且最大值为？如果存在，试求出的值；如果不存在，请说明理由．

【题目】将函数f（x）=sinωx（ω＞0）的图象向左平移 个单位得到函数g（x）的图象，若函数g（x）的图象关于直线x=ω对称且在区间（﹣ω，ω）内单调递增，则ω的值为（ ）
A.
B.
C.
D.

【题目】在平面直角坐标系xOy中，直线l的参数方程为 （t为参数），以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，曲线C的极坐标方程为ρ2= ，且直线l经过曲线C的左焦点F． （ I ）求直线l的普通方程；
（Ⅱ）设曲线C的内接矩形的周长为L，求L的最大值．

【题目】如图1，在直角梯形ABCD中，AD∥BC，AD⊥DC，BC=2AD=2DC，四边形ABEF是正方形．将正方形ABEF沿AB折起到四边形ABE1F1的位置，使平面ABE1F1⊥平面ABCD，M为AF1的中点，如图2．
（I）求证：AC⊥BM；
（Ⅱ）求平面CE1M与平面ABE1F1所成锐二面角的余弦值．

【题目】在数列的每相邻两项之间插入此两项的积，形成新的数列，这样的操作叫做该数列的一次“扩展”．将数列1，2进行“扩展”，第一次得到数列1，2，2；第二次得到数列1，2，2，4，2；…．设第n次“扩展”后所得数列为1，x1 ， x2 ， …，xm ， 2，并记an=log2（1x1x2…xm2），则数列{an}的通项公式为 ．

【题目】已知a＞0，b＞0，函数f（x）=|x+a|+|2x﹣b|的最小值为1．
（1）求证：2a+b=2；
（2）若a+2b≥tab恒成立，求实数t的最大值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网