题目内容
【题目】已知椭圆E:mx2+y2=1(m>0).
(Ⅰ)若椭圆E的右焦点坐标为 ![]() ,求m的值;
,求m的值;
(Ⅱ)由椭圆E上不同三点构成的三角形称为椭圆的内接三角形.若以B(0,1)为直角顶点的椭圆E的内接等腰直角三角形恰有三个,求m的取值范围.
【答案】解:(Ⅰ)椭圆E的方程可以写成 ![]() ,焦点
,焦点 ![]() 在x轴上,所以
在x轴上,所以 ![]() ,b2=1
,b2=1 ![]() ,求得
,求得 ![]() .
.
(Ⅱ)设椭圆E内接等腰直角三角形的两直角边分别为BA,BC,设A(x1,y1),C(x2,y2)
显然BA与BC不与坐标轴平行,且kBAkBC=﹣1<0∴可设直线BA的方程为y=kx+1(k>0),则直线BC的方程为 ![]() ,
,
由 ![]() 消去y得到(m+k2)x2+2kx=0,所以
消去y得到(m+k2)x2+2kx=0,所以 ![]()
求得 ![]()
同理可求 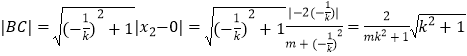
因为△ABC为以B(0,1)为直角顶点的等腰直角三角形,所以|BA|=|BC|,
所以 ![]() ,
,
整理得mk3﹣k2+k﹣m=0(mk3﹣m)﹣(k2﹣k)=0m(k3﹣1)﹣(k2﹣k)=0
m(k﹣1)(k2+k+1)﹣k(k﹣1)=0(k﹣1)[mk2+(m﹣1)k+m]=0
所以k=1或mk2+(m﹣1)k+m=0,设f(k)=mk2+(m﹣1)k+m
因为以B(0,1)为直角顶点的椭圆内接等腰直角三角形恰有三个,
所以关于k的方程mk2+(m﹣1)k+m=0有两个不同的正实根x1,x2,且都不为1∴  ,
,
所以实数m的取值范围是 ![]()
【解析】(Ⅰ)化椭圆E的方程为标准形式,通过焦点 ![]() 在x轴上,求出a,然后求解m即可.(Ⅱ)设椭圆E内接等腰直角三角形的两直角边分别为BA,BC,设A(x1,y1),C(x2,y2),BA与BC不与坐标轴平行,且kBAkBC=﹣1<0,设直线BA的方程为y=kx+1(k>0),则直线BC的方程为
在x轴上,求出a,然后求解m即可.(Ⅱ)设椭圆E内接等腰直角三角形的两直角边分别为BA,BC,设A(x1,y1),C(x2,y2),BA与BC不与坐标轴平行,且kBAkBC=﹣1<0,设直线BA的方程为y=kx+1(k>0),则直线BC的方程为 ![]() ,
,
联立直线与椭圆方程,利用韦达定理以及弦长公式,通过数据线的形状,转化求解即可.

 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案