题目内容
设椭圆 ,右焦点F(c,0),方程
,右焦点F(c,0),方程 的两个根分别为x1,x2,则点P(x1,x2)在 ( )
的两个根分别为x1,x2,则点P(x1,x2)在 ( )
 ,右焦点F(c,0),方程
,右焦点F(c,0),方程 的两个根分别为x1,x2,则点P(x1,x2)在 ( )
的两个根分别为x1,x2,则点P(x1,x2)在 ( )A.圆 上 上 | B.圆 内 内 |
C.圆 外 外 | D.以上三种情况都有可能 |
B
考点:
分析:方程ax2+bx-c=0的两个实数根分别为x1,x2,由韦达定理得:x1+x2=-b/a,x1x2=c/a,x12+x22
=(x1+x2)2-2x1x2= b2 /a2-2c/a ="(" b2-2ac)/ (b2+c2)<1,由此知点P(x1,x2)在圆x2+y2=1内.
解答:解:∵方程ax2+bx-c=0的两个实数根分别为x1,x2,
由韦达定理得:x1+x2=-b/a,x1x2=-c/a,
x12+x22=(x1+x2)2-2x1x2=b2 /a2-2c/a ="(" b2-2ac)/ (b2+c2)<1,
∴点P(x1,x2)在圆x2+y2=1内.
故选A.
点评:本题主要考查椭圆标准方程,简单几何性质,直线与椭圆的位置关系,圆的简单性质等基础知识.考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想.
分析:方程ax2+bx-c=0的两个实数根分别为x1,x2,由韦达定理得:x1+x2=-b/a,x1x2=c/a,x12+x22
=(x1+x2)2-2x1x2= b2 /a2-2c/a ="(" b2-2ac)/ (b2+c2)<1,由此知点P(x1,x2)在圆x2+y2=1内.
解答:解:∵方程ax2+bx-c=0的两个实数根分别为x1,x2,
由韦达定理得:x1+x2=-b/a,x1x2=-c/a,
x12+x22=(x1+x2)2-2x1x2=b2 /a2-2c/a ="(" b2-2ac)/ (b2+c2)<1,
∴点P(x1,x2)在圆x2+y2=1内.
故选A.
点评:本题主要考查椭圆标准方程,简单几何性质,直线与椭圆的位置关系,圆的简单性质等基础知识.考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
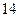 分)
分)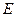 的中心在坐标原点
的中心在坐标原点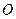 ,两个焦点分别为
,两个焦点分别为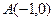 、
、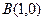 ,一个顶点为
,一个顶点为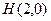 .
.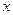 轴上的点
轴上的点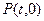 ,椭圆
,椭圆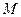 ,使得
,使得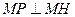 ,求
,求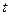 的取值范围.
的取值范围.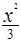 +
+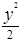 =1上一点P到左焦点的距离为
=1上一点P到左焦点的距离为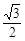 ,则P到右准线的距离为( )
,则P到右准线的距离为( )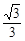
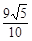

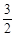
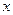 轴上,它的一个顶点恰好是抛物线
轴上,它的一个顶点恰好是抛物线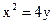 的焦点,离心率
的焦点,离心率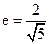 ,过椭圆的右焦点
,过椭圆的右焦点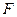 作不与坐标轴垂直的直线
作不与坐标轴垂直的直线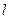 ,交椭圆于A、B两点.
,交椭圆于A、B两点.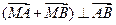 ,求
,求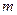 取值范围;
取值范围; 的方程为
的方程为 ,斜率为1的直线
,斜率为1的直线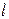 与椭圆
与椭圆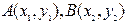 两点.
两点. ,直线
,直线 过点
过点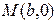 ,且
,且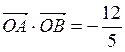 ,求椭圆
,求椭圆 的方程;
的方程; ,若点
,若点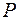 在椭圆
在椭圆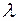 的取值范围.
的取值范围.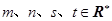 ,
,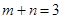 ,
,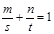 其中
其中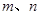 是常数且
是常数且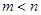 ,若
,若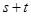 的最小值 是
的最小值 是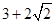 ,满足条件的点
,满足条件的点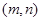 是椭圆
是椭圆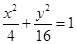 一弦的中点,则此弦所在的直线方程为
一弦的中点,则此弦所在的直线方程为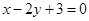
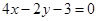
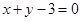
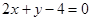
 经过椭圆
经过椭圆 的一个焦点和一个顶点,则该椭圆的离心率为. ( )
的一个焦点和一个顶点,则该椭圆的离心率为. ( )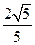
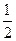

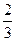
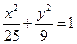
 的两个焦点, 过F1的直线交椭圆于A、B两点, 若
的两个焦点, 过F1的直线交椭圆于A、B两点, 若 , 则 |AB|=" "
, 则 |AB|=" "  上两点间最大的距离为8,则实数
上两点间最大的距离为8,则实数 的值是 ▲
的值是 ▲