题目内容
【题目】公元2222年,有一种高危传染病在全球范围内蔓延,被感染者的潜伏期可以长达10年,期间会有约0.05%的概率传染给他人,一旦发病三天内即死亡,某城市总人口约200万人,专家分析其中约有1000名传染者,为了防止疾病继续扩散,疾病预防控制中心现决定对全市人口进行血液检测以筛选出被感染者,由于检测试剂十分昂贵且数量有限,需要将血样混合后一起检测以节约试剂,已知感染者的检测结果为阳性,末被感染者为阴性,另外检测结果为阳性的血样与检测结果为阴性的血样混合后检测结果为阳性,同一检测结果的血样混合后结果不发生改变.
(1)若对全市人口进行平均分组,同一分组的血样将被混合到一起检测,若发现结果为阳性, 则再在该分组内逐个检测排査,设每个组![]() 个人,那么最坏情况下,需要进行多少次检测可以找到所有的被感染者?在当前方案下,若要使检测的次数尽可能少,每个分组的最优人数?
个人,那么最坏情况下,需要进行多少次检测可以找到所有的被感染者?在当前方案下,若要使检测的次数尽可能少,每个分组的最优人数?
(2)在(1)的检测方案中,对于检测结果为阳性的组来取逐一检测排査的方法并不是很好, 或可将这些组的血样再进行一次分组混合血样检测,然后再进行逐一排査,仍然考虑最坏的情况,请问两次要如何分组,使检测总次数尽可能少?
(3)在(2)的检测方案中,进行了两次分组混合血样检测,仍然考虑最坏情况,若再进行若干次分组混合血样检测,是否会使检测次数更少?请给出最优的检测方案.
【答案】(1)![]() 次,45人;(2)第一次每组159人,第二次每组13人;(3)见解析
次,45人;(2)第一次每组159人,第二次每组13人;(3)见解析
【解析】
(1)根据最坏的情况是1000名被感染者分布在其中1000组里,可得检测总次数,再用基本不等式可得;
(2)设第一次每个组![]() 人,第二次每个组
人,第二次每个组![]() 人,可得检测总次数,再用三元基本不等式,结合整数解可得;
人,可得检测总次数,再用三元基本不等式,结合整数解可得;
(3)设第![]() 次分组中,每组人数为
次分组中,每组人数为![]() ,则可得检测总次数,然后运用
,则可得检测总次数,然后运用![]() 元基本不等式,结合
元基本不等式,结合![]() ,可得
,可得![]() 的最小值,进而得到所求结果.
的最小值,进而得到所求结果.
(1)200万人平均分组,每组![]() 人,总共分
人,总共分![]() 组,每组检测一次,共需检测
组,每组检测一次,共需检测![]() 次,最坏的情况是1000名被感染者分布在其中1000组里,每组一人,然后在这1000组里逐个排查,每组需检测
次,最坏的情况是1000名被感染者分布在其中1000组里,每组一人,然后在这1000组里逐个排查,每组需检测![]() 次,共需检测1000
次,共需检测1000![]() 次,所以找到所有的被感染者共需检测
次,所以找到所有的被感染者共需检测![]()
![]() 次,
次,
由![]()
![]()
![]()
![]() ,
,
当且仅当![]() ,所以
,所以![]()
![]() ,所以
,所以![]()
![]()
![]() 时等号成立.
时等号成立.
由于![]() 为正整数,
为正整数,
所以当![]() 时,
时,![]()
![]() ,
,
当![]() 时,
时,![]()
![]() ,
,
因为![]() ,
,
所以要使检测总次数尽可能少,每个分组的最优人数为45人.
(2)设第一次每个组![]() 人,分
人,分![]() 组;第二次每个组
组;第二次每个组![]() 人,分
人,分![]() 组
组
第一次需检测![]() 次,由(1)的思路知,第二次共需检测
次,由(1)的思路知,第二次共需检测![]()
![]() 次,
次,
所以两次检测的总次数为![]()
![]()
![]() ,
,
因为![]()
![]()
![]()
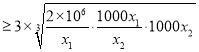
![]()
![]() ,
,
当且仅当![]() ,
,
即![]() ,
,![]() ,
,![]() 时等号成立,
时等号成立,
因为![]()
![]() ,
,![]()
![]() ,且
,且![]() 为正整数,
为正整数,
且![]() ,
,![]() ,
,
所以![]() ,时两次检测的总次数尽可能少,
,时两次检测的总次数尽可能少,
则第一次每个组159人,第二次每个组13人,可使检测总次数尽可能少.
(3)假设进行![]() 次这样的分组检测,可以达到检测次数更少,
次这样的分组检测,可以达到检测次数更少,
设第![]() 次分组中,每组人数为
次分组中,每组人数为![]() ,
,
则总共检测次数为![]() ,
,
因为![]()
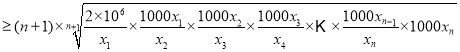
![]() ,
,
当且仅当![]() ,时等号成立,
,时等号成立,
所以![]() ,
,
所以![]() ,
,
所以![]() ,
,
所以![]() ,
,
当![]() 时,
时,![]()
![]()
![]() ,
,
因为![]() ,且
,且![]() 为正整数,
为正整数,
所以可取![]() ,即这样进行了18次检验可得到总次数更小.
,即这样进行了18次检验可得到总次数更小.

【题目】某位同学进行社会实践活动,为了对白天平均气温与某奶茶店的某种饮料销量之间的关系进行分析研究,他分别记录了12月11日至12月15日的白天平均气温![]() (℃)与该小卖部的这种饮料销量
(℃)与该小卖部的这种饮料销量![]() (杯),得到如下数据:
(杯),得到如下数据:
日期 | 12月11日 | 12月12日 | 12月13日 | 12月14日 | 12月15日 |
平均气温 | 9 | 10 | 12 | 11 | 8 |
销量 | 23 | 25 | 30 | 26 | 21 |
(1)请根据所给五组数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)据(1)中所得的线性回归方程,若天气预报12月16日的白天平均气温7(℃),请预测该奶茶店这种饮料的销量. (参考公式: ,
,![]() )
)