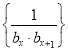题目内容
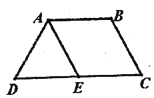
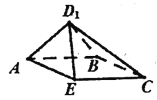
【题目】如图圆锥PO,轴截面PAB是边长为2的等边三角形,过底面圆心O作平行于母线PA的平面,与圆锥侧面的交线是以E为顶点的抛物线的一部分,则该抛物线的焦点到其顶点E的距离为( )

A.1B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
由题可得![]() ,在平面
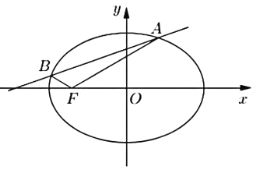
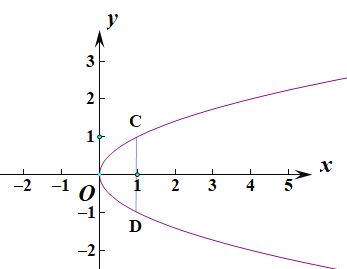
,在平面![]() 内建立直角坐标系.设抛物线的方程为
内建立直角坐标系.设抛物线的方程为![]() ,可得
,可得![]() ,代入解出即可.
,代入解出即可.
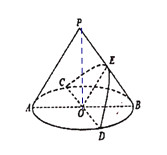
过底面圆心O作平行于母线PA的平面,与圆锥侧面的交线是以E为顶点的抛物线的一部分,![]() 平面PAB, 平面PAB与圆锥的侧面交于OE, 所以OE||PA.
平面PAB, 平面PAB与圆锥的侧面交于OE, 所以OE||PA.
因为OA=OB,所以OE=1=OC,
因为OP⊥底面ABC,所以OP⊥OC,
因为OC⊥OE,OP,OE![]() 平面PAB,OP∩OE=0,
平面PAB,OP∩OE=0,
所以OC⊥平面PAB,所以OC⊥OB.
在平面![]() 内建立直角坐标系.设抛物线的方程为
内建立直角坐标系.设抛物线的方程为![]() ,
,
![]() ,
,
所以该抛物线的焦点到其顶点E的距离为![]()
故选:D

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目