题目内容
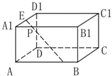 如图,在长方体ABCD-A1B1C1D1中,AA1=1,点E、F分别在棱A1D1,AB上,且线段EF的长恒等于2,则EF的中点P的轨迹是( )
如图,在长方体ABCD-A1B1C1D1中,AA1=1,点E、F分别在棱A1D1,AB上,且线段EF的长恒等于2,则EF的中点P的轨迹是( )分析:连接EA、FA1,PA,PA1,连接PO,O为A1A的中点,由题意说明PA1=PA=1,OP⊥A1A,且OP=
,推出结果.
| ||
| 2 |
解答:解:连接EA、FA1,PA,PA1,如图:
因为几何体是长方体,所以△FA1E,△EAF,都是直角三角形,
点E、F分别在棱A1D1,AB上,且线段EF的长恒等于2,
则EF的中点P满足PA1=PA=1,(直角三角形的斜边上的中线是斜边的一半).
连接PO,O为A1A的中点,∴OP⊥A1A,且OP=
,
所以P的轨迹为以O为圆心,以
为半径的圆的一部分.
故选A.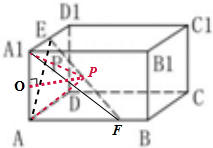
因为几何体是长方体,所以△FA1E,△EAF,都是直角三角形,
点E、F分别在棱A1D1,AB上,且线段EF的长恒等于2,
则EF的中点P满足PA1=PA=1,(直角三角形的斜边上的中线是斜边的一半).
连接PO,O为A1A的中点,∴OP⊥A1A,且OP=
| ||
| 2 |
所以P的轨迹为以O为圆心,以
| ||
| 2 |
故选A.

点评:本题是中档题,考查空间想象能力,逻辑推理能力,作图能力,注意E,F的范围,防止出错.

练习册系列答案
相关题目
 如图在长方体ABCD-A1B1C1D1中,三棱锥A1-ABC的面是直角三角形的个数为:
如图在长方体ABCD-A1B1C1D1中,三棱锥A1-ABC的面是直角三角形的个数为: 如图,定义八个顶点都在某圆柱的底面圆周上的长方体叫做圆柱的内接长方体,圆柱也叫长方体的外接圆柱.设长方体ABCD-A1B1C1D1的长、宽、高分别为a,b,c(其中a>b>c),那么该长方体的外接圆柱侧面积的最大值等于( )
如图,定义八个顶点都在某圆柱的底面圆周上的长方体叫做圆柱的内接长方体,圆柱也叫长方体的外接圆柱.设长方体ABCD-A1B1C1D1的长、宽、高分别为a,b,c(其中a>b>c),那么该长方体的外接圆柱侧面积的最大值等于( )

 .
. 
 ,AA1 =
,AA1 = ,M为侧棱CC1上一点,AM⊥BA1.
,M为侧棱CC1上一点,AM⊥BA1.