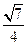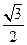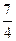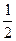题目内容
已知点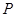 是⊙
是⊙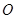 :
: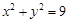 上的任意一点,过
上的任意一点,过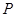 作
作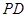 垂直
垂直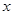 轴于
轴于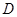 ,动点
,动点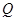 满足
满足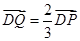 。
。
(1)求动点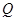 的轨迹方程;
的轨迹方程;
(2)已知点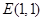 ,在动点
,在动点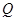 的轨迹上是否存在两个不重合的两点
的轨迹上是否存在两个不重合的两点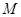 、
、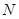 ,使
,使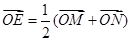 (O是坐标原点),若存在,求出直线
(O是坐标原点),若存在,求出直线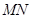 的方程,若不存在,请说明理由。
的方程,若不存在,请说明理由。
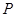 是⊙
是⊙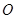 :
: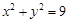 上的任意一点,过
上的任意一点,过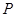 作
作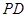 垂直
垂直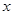 轴于
轴于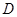 ,动点
,动点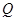 满足
满足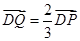 。
。
(1)求动点
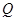 的轨迹方程;
的轨迹方程;(2)已知点
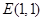 ,在动点
,在动点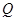 的轨迹上是否存在两个不重合的两点
的轨迹上是否存在两个不重合的两点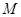 、
、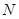 ,使
,使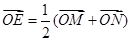 (O是坐标原点),若存在,求出直线
(O是坐标原点),若存在,求出直线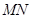 的方程,若不存在,请说明理由。
的方程,若不存在,请说明理由。(1)
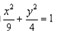
(2)
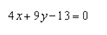
(1)设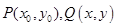 ,依题意,则点
,依题意,则点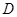 的坐标为
的坐标为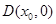
∴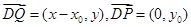 2分
2分


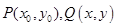 ,依题意,则点
,依题意,则点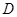 的坐标为
的坐标为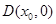
∴
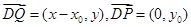 2分
2分


练习册系列答案
相关题目
 且椭圆经过
且椭圆经过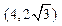 .
.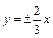 ,经过点
,经过点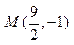 .
.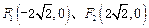 ,长轴长为6,
,长轴长为6,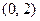 且斜率为1的直线交椭圆C于A 、B两点,求线段AB的长度.
且斜率为1的直线交椭圆C于A 、B两点,求线段AB的长度.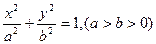 的左焦点,A(-a,0), B(0,b), 椭圆的离心率为
的左焦点,A(-a,0), B(0,b), 椭圆的离心率为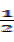 , 点D在x轴上,
, 点D在x轴上,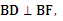 B,D,F三点确定的圆M恰好与直线l1:x+
B,D,F三点确定的圆M恰好与直线l1:x+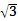 y+30相切
y+30相切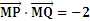 ,求直线l2的方程
,求直线l2的方程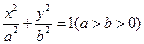 的离心率为
的离心率为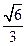 ,短轴的一个端点到右焦点的距离为
,短轴的一个端点到右焦点的距离为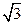 ,直线
,直线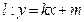 交椭圆于不同的两点
交椭圆于不同的两点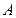 ,
,
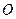 到直线
到直线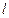 的距离为
的距离为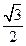 ,求
,求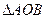 面积的最大值
面积的最大值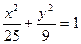 ,直线
,直线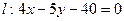 .椭圆上是否存在一点,它到直线
.椭圆上是否存在一点,它到直线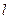 的距离最小?最小距离是多少?
的距离最小?最小距离是多少?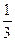 ,则椭圆方程
,则椭圆方程 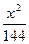 +
+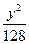 ="1"
="1"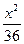 +
+ ="1"
="1"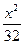 +
+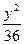 ="1"
="1"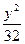 =1
=1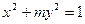 的焦点在
的焦点在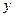 轴上,长轴长是短轴长的两倍,则
轴上,长轴长是短轴长的两倍,则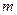 的值为( )
的值为( )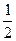
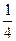
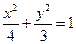 的离心率为
的离心率为