题目内容
【题目】[选修4-5：不等式选讲]
已知函数f（x）=x+1+|3﹣x|，x≥﹣1．
（I）求不等式f（x）≤6的解集；
（Ⅱ）若f（x）的最小值为n，正数a，b满足2nab=a+2b，求2a+b的最小值．
【答案】解：（Ⅰ）根据题意，函数f（x）=x+1+|3﹣x|，x≥﹣1． 若f（x）≤6，则有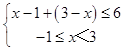 
或 
，
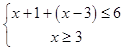解可得﹣1≤x≤4，
故原不等式的解集为{x|﹣1≤x≤4}；
（Ⅱ）函数f（x）=x+1+|3﹣x|= 
，
分析可得f（x）的最小值为4，即n=4；
则正数a，b满足8ab=a+2b，即 
=8，
2a+b= 
（ ）（2a+b）= （ 
+5）≥ （5+2 
）= 
；
即2a+b的最小值为 ．
【解析】（Ⅰ）根据题意，由绝对值的性质可以将f（x）≤6转化可得 
或 
，解可得x的范围，即可得答案；（Ⅱ）根据题意，由函数f（x）的解析式分析可得f（x）的最小值为4，即n=4；进而可得正数a，b满足8ab=a+2b，即 
=8，将2a+b变形可得2a+b= 
（ 
+5），由基本不等式的性质可得2a+b的最小值，即可得答案．
【考点精析】根据题目的已知条件，利用绝对值不等式的解法的相关知识可以得到问题的答案，需要掌握含绝对值不等式的解法：定义法、平方法、同解变形法，其同解定理有；规律：关键是去掉绝对值的符号．
练习册系列答案
相关题目
