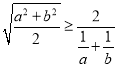题目内容
【题目】已知函数![]() .
.
(1)若![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(2)求证:![]() 时,
时,![]() .
.
【答案】(1)![]() (2)证明见解析
(2)证明见解析
【解析】
(1)通过换元法,将不等式![]() 恒成立转化为
恒成立转化为![]() 恒成立,其中
恒成立,其中![]() .构造函数
.构造函数![]() ,利用导数研究
,利用导数研究![]() 的单调性,结合
的单调性,结合![]() 三种情况进行分类讨论,由此求得实数
三种情况进行分类讨论,由此求得实数![]() 的取值范围.
的取值范围.
(2)利用分析法,将所要证明的不等式转化为证明![]() ,结合(1)的结论以及基本不等式,证得上述不等式成立.
,结合(1)的结论以及基本不等式,证得上述不等式成立.
(1)![]() .
.
记![]() ,原不等式转化为
,原不等式转化为![]() 恒成立,其中
恒成立,其中![]() .
.
令![]() ,则
,则![]() ,
,
记![]() ,则
,则![]() .
.
①当![]() 时,注意到
时,注意到![]() ,故
,故![]() 恒成立,从而
恒成立,从而![]() .
.
于是,函数![]() 在
在![]() 上单调减,
上单调减,![]() ,符合题意;
,符合题意;
②当![]() 时,考虑
时,考虑![]() 时,
时,![]() 恒成立,即函数
恒成立,即函数![]() 在
在![]() 上单调增,所以,
上单调增,所以,![]() 时,
时,![]() ,不符合题意,舍去.
,不符合题意,舍去.
③当![]() 时,
时,![]() ,
,![]() ,不符合题意,舍去.
,不符合题意,舍去.
综上,实数![]() 的取值范围是
的取值范围是![]() .
.
(2)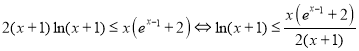 .
.
由(1)的过程知![]() ,即
,即![]() .
.
故要证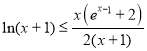 ,只需证
,只需证![]() (*).
(*).
事实上,由(1)的结论知,当![]() 时,
时,![]() 恒成立,即
恒成立,即![]() 时,
时,![]() ,而
,而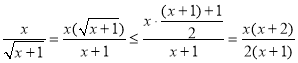 ,即(*)成立,
,即(*)成立,
等号当且仅当![]() 时取到,故原不等式获证.
时取到,故原不等式获证.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】2020年春,新型冠状病毒在我国湖北武汉爆发并讯速蔓延,病毒传染性强并严重危害人民生命安全,国家卫健委果断要求全体人民自我居家隔离,为支援湖北武汉新型冠状病毒疫情防控工作,各地医护人员纷纷逆行,才使得病毒蔓延得到了有效控制.某社区为保障居民的生活不受影响,由社区志愿者为其配送蔬菜、大米等生活用品,记者随机抽查了男、女居民各100名对志愿者所买生活用品满意度的评价,得到下面的2×2列联表.
特别满意 | 基本满意 | |
男 | 80 | 20 |
女 | 95 | 5 |
(1)被调查的男性居民中有5个年轻人,其中有2名对志愿者所买生活用品特别满意,现在这5名年轻人中随机抽取3人,求至多有1人特别满意的概率.
(2)能否有99%的把握认为男、女居民对志愿者所买生活用品的评价有差异?
附: 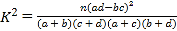
|
|
|
|
|
|
|
|