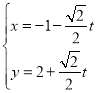题目内容
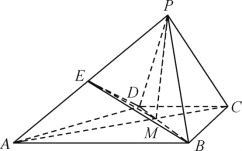
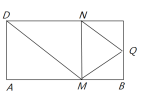
【题目】已知圆锥的顶点为A,高和底面的半径相等,BE是底面圆的一条直径,点D为底面圆周上的一点,且∠ABD=60°,则异面直线AB与DE所成角的正弦值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
根据圆锥高和底面的半径相等,且点D为底面圆周上的一点,∠ABD=60,可知D为![]() 的中点,则以底面中心为原点,分别以OD,OE,OA为x,y,z轴,建立空间直角坐标系,不妨设底面半径为1,求得向量
的中点,则以底面中心为原点,分别以OD,OE,OA为x,y,z轴,建立空间直角坐标系,不妨设底面半径为1,求得向量![]() ,
,![]() 的坐标,代入公式cos
的坐标,代入公式cos![]() ,
,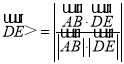 求解.
求解.
因为高和底面的半径相等,∴OE=OB=OA,OA⊥底面DEB.
∵点D为底面圆周上的一点,且∠ABD=60°,
∴AB=AD=DB;
∴D为![]() 的中点
的中点
建立如图所示空间直角坐标系,
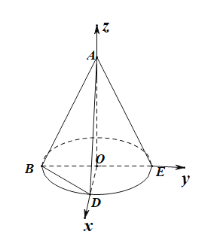
不妨设OB=1.
则O(0,0,0),B(0,﹣1,0),D(1,0,0),A(0,0,1),E(0,1,0),
∴![]() (0,﹣1,﹣1),
(0,﹣1,﹣1),![]() (﹣1,1,0),
(﹣1,1,0),
∴cos![]() ,
,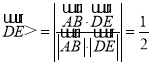 ,
,
∴异面直线AM与PB所成角的大小为![]() .
.
∴异面直线AB与DE所成角的正弦值为![]() .
.
故选:A.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目