题目内容
如图,在四棱锥P-ABCD中,四边形ABCD是正方形,PD⊥平面ABCD,PD=AB=2, E,F,G分别是PC,PD,BC的中点.
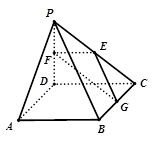
(1)求三棱锥E-CGF的体积;
(2)求证:平面PAB//平面EFG;

(1)求三棱锥E-CGF的体积;
(2)求证:平面PAB//平面EFG;
(1)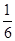 (2)对于面面平行的证明,一般要根据判定定理来得到,先证明EG//平面PAB.来说民结论。
(2)对于面面平行的证明,一般要根据判定定理来得到,先证明EG//平面PAB.来说民结论。
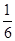 (2)对于面面平行的证明,一般要根据判定定理来得到,先证明EG//平面PAB.来说民结论。
(2)对于面面平行的证明,一般要根据判定定理来得到,先证明EG//平面PAB.来说民结论。试题分析:(1)解:∵PD⊥平面ABCD,
∴PD⊥BC.
又∵ABCD为正方形,
∴CD⊥BC,
∴BC⊥平面PCD即GC⊥平面CEF.
∴VE-CGF= VG-CEF=
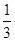 ×S△CEF×GC=
×S△CEF×GC=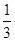 ×(
×(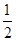 ×1×1)×1=
×1×1)×1=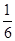 . 3分
. 3分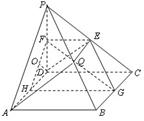
(2)证明:E,F分别是线段PC,PD的中点,
∴EF//CD.
又ABCD为正方形,AB//CD,
∴EF//AB.
又EF
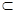 平面PAB,
平面PAB,∴EF//平面PAB.
∵E,G分别是线段PC,BC的中点,
∴EG//PB.
又EG
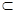 平面PAB,
平面PAB,∴EG//平面PAB.
∵EF∩EG=E,
∴平面PAB//平面EFG. 6分
(3)Q为线段PB中点时,PC⊥平面ADQ.
取PB中点Q,连接DE,EQ,AQ,
∵EQ//BC//AD,
∴ADEQ为平面四边形,
由PD⊥平面ABCD,得AD⊥PD,
又AD⊥CD,PD∩CD=D,
∴AD⊥平面PDC,∴AD⊥PC,
又三角形PDC为等腰直角三角形,E为斜边中点,
∴DE⊥PC.
∵AD∩DE=D,
∴PC⊥平面ADQ. 10分
点评:主要是考查了几何体的体积的计算,以及线面平行的判定定理的运用,属于中档题。

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案
相关题目
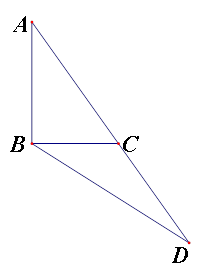
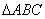 中,
中,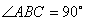 ,延长
,延长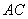 到
到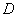 ,连接
,连接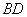 ,若
,若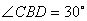 ,且
,且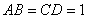 ,则
,则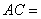 ________.
________.
 中,
中,  ,
, ,则二面角
,则二面角 的余弦值为
的余弦值为



 中,M、N分别是棱CD1、CC1的中点,则异面直线MA1与DN所成角的余弦值是 .
中,M、N分别是棱CD1、CC1的中点,则异面直线MA1与DN所成角的余弦值是 . β且α⊥β,则l⊥α
β且α⊥β,则l⊥α β=m,且l∥m, 则l∥α
β=m,且l∥m, 则l∥α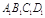 的底面
的底面 为菱 形 ,AC∩BD=O侧棱
为菱 形 ,AC∩BD=O侧棱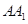 ⊥BD,点F为
⊥BD,点F为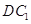 的中点.
的中点.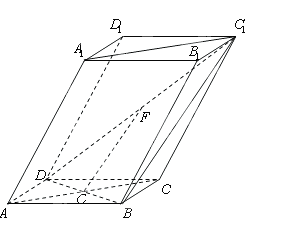
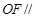 平面
平面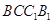 ;
;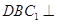 平面
平面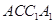 .
. 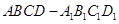 中,设
中,设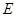 是棱
是棱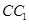 的中点.
的中点.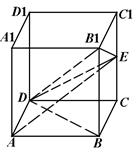
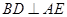 ;
;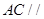 平面
平面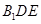 ;
;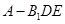 的体积.
的体积.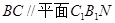 ; (2)求证:
; (2)求证: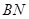
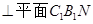 ;
; 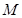 为
为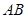 中点,在
中点,在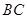 边上找一点
边上找一点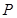 ,使
,使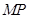
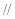 平面
平面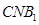 ,并求
,并求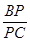 的值.
的值.