题目内容
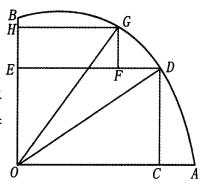
【题目】如图为某大河的一段支流,岸线![]() 近似满足
近似满足![]() ∥
∥![]() 宽度为7
宽度为7![]() 圆
圆![]() 为河中的一个半径为2
为河中的一个半径为2![]() 的小岛,小镇
的小岛,小镇![]() 位于岸线
位于岸线![]() 上,且满足岸线
上,且满足岸线![]() 现计划建造一条自小镇
现计划建造一条自小镇![]() 经小岛
经小岛![]() 至对岸
至对岸![]() 的通道
的通道![]() (图中粗线部分折线段,
(图中粗线部分折线段,![]() 在
在![]() 右侧),为保护小岛,
右侧),为保护小岛,![]() 段设计成与圆
段设计成与圆![]() 相切,设
相切,设![]()
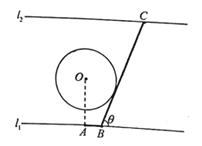
(1)试将通道![]() 的长
的长![]() 表示成
表示成![]() 的函数,并指出其定义域.
的函数,并指出其定义域.
(2)求通道![]() 的最短长.
的最短长.
【答案】(1)![]() (2)
(2) ![]()
【解析】
(1) 过![]() 点作
点作![]() 于
于![]() 点,以
点,以![]() 为原点,建立如图所示的直角坐标系,先求出
为原点,建立如图所示的直角坐标系,先求出![]() ,
,
再求出![]() ,即可求出
,即可求出![]() ,再求函数的定义域.(2)利用导数求函数的最小值,即得通道ABC的最短长.
,再求函数的定义域.(2)利用导数求函数的最小值,即得通道ABC的最短长.
(1)过![]() 点作
点作![]() 于
于![]() 点,
点,
因为![]() 与
与![]() 的距离为
的距离为![]() ,
,
所以![]() ,
,
以![]() 为原点,建立如图所示的直角坐标系,
为原点,建立如图所示的直角坐标系,
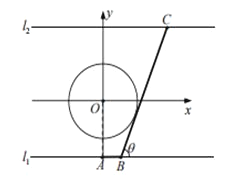
因为![]() ,所以设
,所以设![]() ,
,
则直线![]() 的方程为
的方程为![]() ,即
,即![]()
因为![]() 与圆
与圆![]() 相切,圆
相切,圆![]() 的半径为
的半径为![]() ,
,
所以![]() ,
,
因为![]() ,所以
,所以![]() ,
,
即![]() ,
,
所以![]() ,
,
由于![]() ,所以
,所以![]() ,
,
令![]() ,
,
则因为函数![]() 在
在![]() 上单调递减,所以
上单调递减,所以![]() ,
,
即函数![]() 的定义域为
的定义域为![]() .
.
(2![]()
令![]() ,得
,得![]() ,则
,则![]() ,其中
,其中![]() ,且
,且![]() .
.
由![]() ,得
,得![]() ,
,
|
|
|
|
|
| 0 | + |
|
| 极小值 |
|
所以当![]() 时,
时,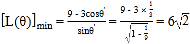 ,
,
即通道![]() 的最短长为
的最短长为![]() .
.

练习册系列答案
相关题目