题目内容
过点(0,1)作直线,使它与抛物线y2=4x仅有一个公共点,这样的直线有( )
| A.1条 | B.2条 | C.3条 | D.4条 |
C
设过点(0,1)斜率为k的直线方程为y=kx+1.
由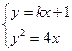 得k2x2+(2k-4)x+1=0.(*)
得k2x2+(2k-4)x+1=0.(*)
当k=0时,(*)式只有一个根;
当k≠0时,Δ=(2k-4)2-4k2=-16k+16,
由Δ=0,即-16k+16=0得k=1.
所以k=0,或k=1时,直线与抛物线只有一个公共点,
又直线x=0和抛物线只有一个公共点.选C.
由
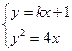 得k2x2+(2k-4)x+1=0.(*)
得k2x2+(2k-4)x+1=0.(*)当k=0时,(*)式只有一个根;
当k≠0时,Δ=(2k-4)2-4k2=-16k+16,
由Δ=0,即-16k+16=0得k=1.
所以k=0,或k=1时,直线与抛物线只有一个公共点,
又直线x=0和抛物线只有一个公共点.选C.

练习册系列答案
相关题目
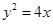 .
.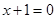 相切,求所有的圆都经过的定点坐标;
相切,求所有的圆都经过的定点坐标;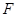 ,若过
,若过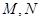 两点,若
两点,若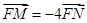 ,求直线
,求直线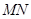 的斜率;
的斜率;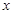 正半轴上
正半轴上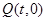 点的直线与该抛物线交于
点的直线与该抛物线交于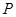 为抛物线上异于
为抛物线上异于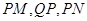 连线的斜率为
连线的斜率为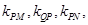 试求满足
试求满足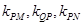 成等差数列的充要条件.
成等差数列的充要条件.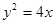 ,直线
,直线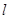 的方程为
的方程为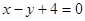 ,在抛物线上有一动点P到y轴的距离为
,在抛物线上有一动点P到y轴的距离为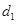 ,P到直线
,P到直线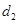 ,则
,则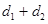 的最小值为( )
的最小值为( ) 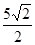


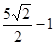
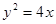 的顶点作射线
的顶点作射线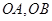 与抛物线交于
与抛物线交于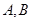 ,若
,若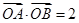 ,求证:直线
,求证:直线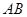 过定点.
过定点.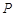 与定点
与定点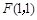 和直线
和直线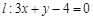 的距离相等,则动点
的距离相等,则动点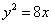 上到其焦点
上到其焦点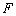 距离为5的点有( )
距离为5的点有( )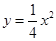 的焦点坐标是( )
的焦点坐标是( )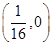
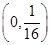
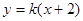 (k>0)与抛物线
(k>0)与抛物线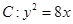 相交于
相交于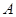 、
、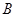 两点,
两点,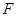 为
为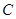 的焦点,若
的焦点,若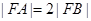 ,则k的值为( )
,则k的值为( )