题目内容
设抛物线C：y2＝2px(p>0)的焦点为F，点M在C上，|MF|＝5，若以MF为直径的圆过点(0,2)，则C的方程为( )
【选项】
【选项】
| A．y2＝4x或y2＝8x |
| B．y2＝2x或y2＝8x |
| C．y2＝4x或y2＝16x |
| D．y2＝2x或y2＝16x |
C
由题意知：F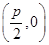
，抛物线的准线方程为x＝－
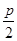，则由抛物线的定义知，xM＝5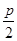－，设以MF为直径的圆的圆心为
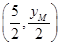，所以圆的方程为
＋
＝
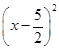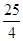，又因为圆过点(0,2)，所以yM＝4，又因为点M在C上，所以16＝
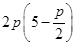，解得p＝2或p＝8，所以抛物线C的方程为y2＝4x或y2＝16x，选C.
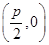，抛物线的准线方程为x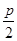＝－，则由抛物线的定义知，xM＝5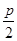－，设以MF为直径的圆的圆心为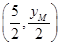，所以圆的方程为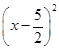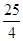＋＝，又因为圆过点(0,2)，所以yM＝4，又因为点M在C上，所以16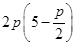＝，解得p＝2或p＝8，所以抛物线C的方程为y2＝4x或y2＝16x，选C.
练习册系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
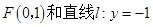，过点F且与直线
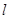相切的动圆圆心为点M，记点M的轨迹为曲线E.
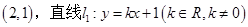，与曲线E相交于B，C两点，直线AB，AC分别交直线
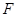是抛物线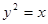 
的焦点，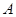
、
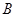是该抛物线上的两点，
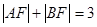,则线段
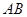的中点到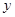
轴的距离为（ ）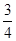
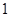
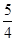
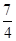
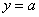交抛物线
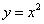于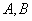
两点．若该抛物线上存在点
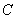，使得
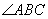为直角，则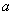
的取值范围为________．
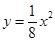的焦点坐标为_________________;