题目内容
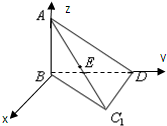
如图,在平行四边形ABCD中,AB=1,BD=
,∠ABD=90°,将它们沿对角线BD折起,折后的点C变为C1,且AC1=2.
(1)求证:平面ABD⊥平面BC1D;
(2)E为线段AC1上的一个动点,当线段EC1的长为多少时,DE与平面BC1D所成的角为30°?

| 2 |
(1)求证:平面ABD⊥平面BC1D;
(2)E为线段AC1上的一个动点,当线段EC1的长为多少时,DE与平面BC1D所成的角为30°?

(1)证明:∵AB=1,BD=
,∠ABD=90°,∴AD=
=
=BC,
∵AC1=2,∴AC12=AB2+BC12,∴∠ABC1=90°,∴AB⊥BC1.
又AB⊥BD,BC1∩BD=B,∴AB⊥平面BC1D,
∵AB?平面ABD,∴平面ABD⊥平面BC1D.
(2)在平面BC1D过点B作直线l⊥BD,分别以直线l,BD,BA为x,y,z建立空间直角坐标系B-xyz,
则A(0,0,1),C1(1,
,0),D(0,
,0),
∴
=(1,
,-1),
=(0,0,1),
设
=λ
=(λ,
λ,-λ),则E(λ,
λ,1-λ),λ∈[0,1],∴
=(λ,
λ-
,1-λ).
又
=(0,0,1)是平面BC1D的一个法向量,
依题意得sin30o=|cos<
,
>|,即|
|=
,
解得λ=
,即|C1E|=1时,DE与平面BC1D所成的角为30°.
| 2 |
12+(
|
| 3 |
∵AC1=2,∴AC12=AB2+BC12,∴∠ABC1=90°,∴AB⊥BC1.
又AB⊥BD,BC1∩BD=B,∴AB⊥平面BC1D,
∵AB?平面ABD,∴平面ABD⊥平面BC1D.
(2)在平面BC1D过点B作直线l⊥BD,分别以直线l,BD,BA为x,y,z建立空间直角坐标系B-xyz,
则A(0,0,1),C1(1,
| 2 |
| 2 |
∴
| AC1 |
| 2 |
| BA |
设
| AE |
| AC1 |
| 2 |
| 2 |
| DE |
| 2 |
| 2 |
又
| BA |
依题意得sin30o=|cos<
| BA |
| DE |
| 1-λ | ||
|
| 1 |
| 2 |
解得λ=
| 1 |
| 2 |


练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目






 =
= ,
, =
= ,且|
,且|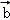 |等于( )
|等于( )
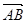 +
+ +
+ = .
= .