题目内容
已知抛物线y2=2px(p>0)与一个定点M(p,p),则抛物线上与M点的距离最小的点为( )
| A.(0,0) | B.(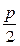 ,p) ,p) | C.(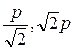 ) ) | D.( ) ) |
D
设抛物线上的任意点(x,y)到点M的距离为d,则有
d2=(p-x)2+(p-y)2=(p-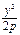 )2+(p-y)2.
)2+(p-y)2.
∴(d2)′=2(p-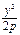 )(-
)(-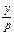 )+2(p-y)(-1)=
)+2(p-y)(-1)=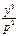 -2p.
-2p.
令(d2)′y=0,即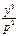 -2p=0,解得y=
-2p=0,解得y=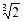 p.这是函数在定义域内的唯一极值点,所以必是最值点.代入抛物线方程得
p.这是函数在定义域内的唯一极值点,所以必是最值点.代入抛物线方程得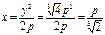 .所以点(
.所以点(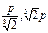 )为所求的点.故选D
)为所求的点.故选D
d2=(p-x)2+(p-y)2=(p-
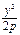 )2+(p-y)2.
)2+(p-y)2.∴(d2)′=2(p-
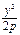 )(-
)(-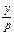 )+2(p-y)(-1)=
)+2(p-y)(-1)=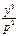 -2p.
-2p.令(d2)′y=0,即
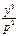 -2p=0,解得y=
-2p=0,解得y=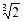 p.这是函数在定义域内的唯一极值点,所以必是最值点.代入抛物线方程得
p.这是函数在定义域内的唯一极值点,所以必是最值点.代入抛物线方程得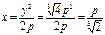 .所以点(
.所以点(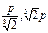 )为所求的点.故选D
)为所求的点.故选D
练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
 是定义在
是定义在 上的奇函数,且当
上的奇函数,且当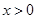 时,
时,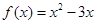 ,则
,则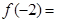 ( )
( )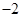
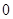
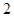
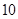
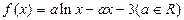
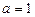 时,求函数
时,求函数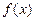 的单调区间;
的单调区间;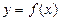 的图像在点
的图像在点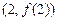 处的切线的倾斜角为
处的切线的倾斜角为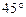 ,问:
,问: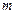 在什么范围取值时,函数
在什么范围取值时,函数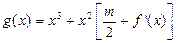 在区间
在区间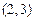 上总存在极值?
上总存在极值?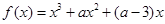 的导函数是
的导函数是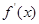 ,若
,若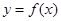 在原点处的切线方程为( )
在原点处的切线方程为( )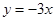
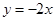
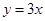
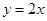
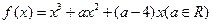 的导函数
的导函数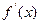 是偶函数,则曲线
是偶函数,则曲线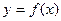 在原点处的切线方程是( )
在原点处的切线方程是( )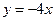
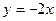
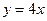
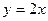
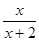 在点(-1,-1)处的切线方程为(......)
在点(-1,-1)处的切线方程为(......)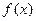 的定义域为D,如果存在正实数
的定义域为D,如果存在正实数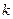 ,使对任意
,使对任意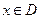 ,都有
,都有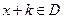 ,且
,且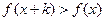 恒成立,则称函数
恒成立,则称函数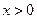 时,
时, ,若
,若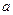 的取值范围是 .
的取值范围是 . 在点
在点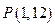 处的切线方程是
处的切线方程是