题目内容
14.下列各函数中,最小值为2的是( )| A. | y=x+$\frac{1}{x}$ | B. | y=sinx+$\frac{1}{sinx}$,x∈(0,$\frac{π}{2}$) | ||
| C. | y=$\frac{{{x^2}+3}}{{\sqrt{{x^2}+2}}}$ | D. | y=5x+5-x |
分析 由基本不等式求最值的规则,逐个选项验证可得.
解答 解:选项A,x可能为负数,不满足最小值为2,故错误;
选项B,当且仅当sinx=1时才会使最小值为2,而x∈(0,$\frac{π}{2}$)时,sinx取不到1,故错误;
选项C,y=$\frac{{{x^2}+3}}{{\sqrt{{x^2}+2}}}$=$\frac{{x}^{2}+2+1}{\sqrt{{x}^{2}+2}}$=$\sqrt{{x}^{2}+2}$+$\frac{1}{\sqrt{{x}^{2}+2}}$≥2,当且仅当$\sqrt{{x}^{2}+2}$=$\frac{1}{\sqrt{{x}^{2}+2}}$
即x2+2=1即x2=-1时取等号,显然任意实数x不满足x2=-1,故错误;
选项D,由基本不等式可得y=5x+5-x≥2$\sqrt{{5}^{x}•{5}^{-x}}$=2,当且仅当5x=5-x≥x=0时取等号,故正确.
故选:D
点评 本题考查基本不等式求最值,注意等号成立的条件是解决问题的关键,属基础题.

练习册系列答案
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案
相关题目
9.C${\;}_{6}^{1}$+C${\;}_{6}^{2}$+C${\;}_{6}^{3}$+C${\;}_{6}^{4}$+C${\;}_{6}^{5}$的值为( )
| A. | 64 | B. | 63 | C. | 62 | D. | 61 |
19.在△ABC中,b=1,c=$\sqrt{3}$,B=30°,则C的大小为( )
| A. | 30° | B. | 30°或150° | C. | 60°或120° | D. | 60° |
6.设函数f(x)=-x2+2x+3,x∈[-5,5].若从区间内随机选取一个实数x0,则所选取的实数x0满足f(x0)≤0的概率为( )
| A. | 0.3 | B. | 0.4 | C. | 0.5 | D. | 0.6 |
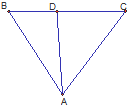 如图,已知A,B,C三点不共线.
如图,已知A,B,C三点不共线.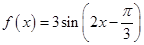 的图象为
的图象为 ,下列结论中正确的是( )
,下列结论中正确的是( ) 对称
对称 对称
对称 在区间
在区间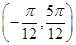 上递增
上递增 的图象向右平移
的图象向右平移 个单位长度可得
个单位长度可得 中,角
中,角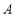 ,
, ,
, 所对的边分别为
所对的边分别为 ,
, ,
, 满足
满足 ,
, ,
,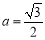 ,则
,则 的取值范围是( )
的取值范围是( ) B.
B.
 D.
D.