题目内容
12.已知函数f(x)=$\frac{a+lnx}{x}$在点(1,f(1))处切线与x轴平行.求实数a的值及f(x)的极值.分析 求函数的导数,根据导数的几何意义建立条件关系即可求实数a的值及f(x)的极值.
解答 解:函数的f(x)的导数f′(x)=$\frac{\frac{1}{x}•x-(a+lnx)}{{x}^{2}}$=$\frac{1-a-lnx}{{x}^{2}}$,
∵f(x)在点(1,f(1))处的切线与x轴平行,
∴f′(1)=$\frac{1-a-ln1}{{1}^{2}}$=0,
∴a=1,
∴f(x)=$\frac{1+lnx}{x}$,
f′(x)=-$\frac{lnx}{{x}^{2}}$,
当0<x<1时,f′(x)>0,当x>1时,f′(x)<0,
∴f(x)在(0,1)上单调递增,在(1,+∞)单调递减,
故f(x)在x=1处取得极大值1,无极小值.
点评 本题主要考查导数的综合应用,根据导数的几何意义求出a,以及函数极值,属于中档题.

练习册系列答案
相关题目
17.在样本的频率分布直方图中,共有n个小矩形,若中间一个小矩形的面积等于其余(n-1)个矩形面积的$\frac{1}{5}$,且频数为50,则样本容量为( )
| A. | 500 | B. | 300 | C. | 480 | D. | 360 |
4.设△ABC的内角A,B,C所对应的边分别是a,b,c,若A=60°,a=$\sqrt{13}$,b=4,则c=( )
| A. | 1 | B. | 3 | C. | 1或3 | D. | 无解 |
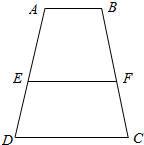 在梯形ABCD中,AB=a,CD=b,a<b,EF为一线段,若S四边形ABFE=S四边形CDEF,且∠BFE=∠D,求EF的长(用a,b表示).
在梯形ABCD中,AB=a,CD=b,a<b,EF为一线段,若S四边形ABFE=S四边形CDEF,且∠BFE=∠D,求EF的长(用a,b表示).