题目内容
(本小题满分14分)
已知数列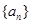 的前
的前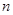 项和
项和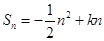 ,
,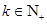 ,且
,且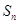 的最大值为8.
的最大值为8.
(1)确定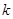 的值;
的值;
(2)求数列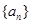 的通项公式;
的通项公式;
(3)求数列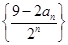 的前
的前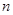 项和
项和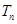 .
.
已知数列
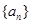 的前
的前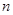 项和
项和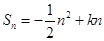 ,
,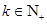 ,且
,且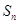 的最大值为8.
的最大值为8.(1)确定
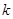 的值;
的值;(2)求数列
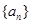 的通项公式;
的通项公式;(3)求数列
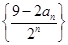 的前
的前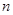 项和
项和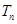 .
.(1)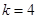 ;(2)
;(2)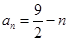 ;(3)
;(3)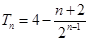 。
。
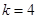 ;(2)
;(2)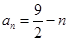 ;(3)
;(3)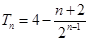 。
。本题主要考查了由数列的递推公式求解数列的通项公式,及数列求和的错位相减求和方法是数列求和中的重要方法,也是高考在数列部分(尤其是理科)考查的热点,要注意掌握。
(1)由二次函数的性质可知,当n=k时,Sn=-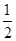 n2+kn取得最大值,代入可求k,然后利用an=sn-sn-1可求通项
n2+kn取得最大值,代入可求k,然后利用an=sn-sn-1可求通项
(2)由bn=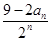 ,可利用错位相减求和即可。
,可利用错位相减求和即可。
解:(1)∵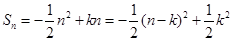 ,又
,又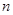 ,
,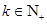 ,所以当
,所以当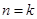 时,
时,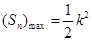 ,由题设
,由题设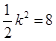 ,
,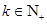 ,故
,故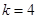 ;…………4分
;…………4分
(2)由(1)得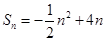 ;当
;当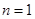 时,
时,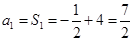 ;…………6分
;…………6分
当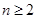 时,
时,
因为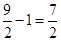 ,所以
,所以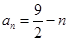 也满足
也满足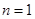 ,
,
即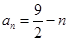 …………………9分
…………………9分
(3)∵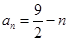 ,∴
,∴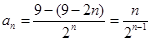 ,故
,故
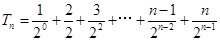 …………①…………10分
…………①…………10分
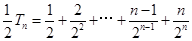 …………②………………11分
…………②………………11分
由①?②得: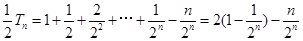 ,故
,故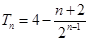 ……14分
……14分
(1)由二次函数的性质可知,当n=k时,Sn=-
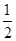 n2+kn取得最大值,代入可求k,然后利用an=sn-sn-1可求通项
n2+kn取得最大值,代入可求k,然后利用an=sn-sn-1可求通项(2)由bn=
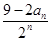 ,可利用错位相减求和即可。
,可利用错位相减求和即可。解:(1)∵
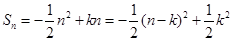 ,又
,又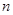 ,
,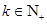 ,所以当
,所以当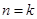 时,
时,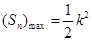 ,由题设
,由题设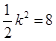 ,
,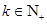 ,故
,故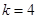 ;…………4分
;…………4分(2)由(1)得
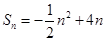 ;当
;当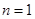 时,
时,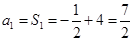 ;…………6分
;…………6分当
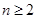 时,
时,
因为
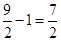 ,所以
,所以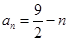 也满足
也满足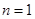 ,
,即
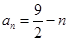 …………………9分
…………………9分(3)∵
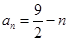 ,∴
,∴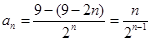 ,故
,故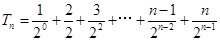 …………①…………10分
…………①…………10分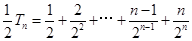 …………②………………11分
…………②………………11分由①?②得:
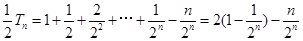 ,故
,故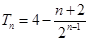 ……14分
……14分
练习册系列答案
相关题目
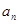 }的前n项和为
}的前n项和为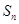 , 满足
, 满足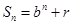 (
(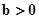
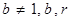 均为常数)
均为常数)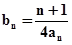
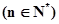 ,求数列
,求数列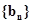 的前
的前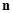 项的和
项的和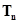 .(6分)
.(6分)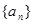 满足
满足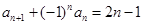 ,则
,则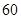 项和为
项和为 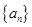 中,
中,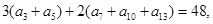 则等差数列
则等差数列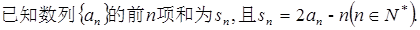
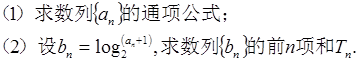
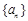 是公比为q的等比数列,且
是公比为q的等比数列,且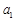 ,
,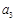 ,
,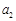 成等差数列,则q=
成等差数列,则q=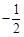
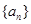 是一个公差大于
是一个公差大于 的等差数列,且满足
的等差数列,且满足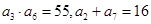 .数列
.数列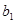 ,
,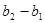 ,
,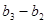 ,…,
,…,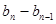 是首项为
是首项为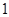 ,公比为
,公比为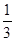 的等比数列.
的等比数列.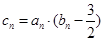 ,求数列
,求数列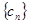 的前
的前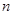 项和
项和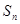 .
.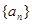 、
、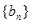 都是公差为1的等差数列,其首项分别为
都是公差为1的等差数列,其首项分别为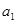 、
、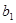 ,且
,且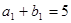 ,
, 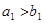 ,
,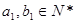 ,
,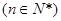 ,则数列
,则数列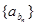 前10项的和等于( )
前10项的和等于( )