题目内容
等差数列{an}中,a1+3a8+a15=120,则2a6-a4的值为
24
本试题主要是考查了等差数列的通项公式的运用,以及等差中项的性质的运算。
因为等差数列{an}中,根据等差中项的性质可知,a1+a15=2a8,所以a1+3a8+a15=120=5 a8,a8=24,因为a4+a8=2a6,所以2a6-a4=a8=24,故填写为24.
解决该试题的关键是运用通项公式得到第8项。然后根据中项性质得到。
因为等差数列{an}中,根据等差中项的性质可知,a1+a15=2a8,所以a1+3a8+a15=120=5 a8,a8=24,因为a4+a8=2a6,所以2a6-a4=a8=24,故填写为24.
解决该试题的关键是运用通项公式得到第8项。然后根据中项性质得到。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
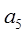 =10,且
=10,且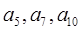 是等比数列{
是等比数列{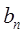 }的第1,3,5项,且
}的第1,3,5项,且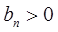 .
.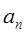 }的第20项,(2)求数列{
}的第20项,(2)求数列{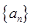 中,
中, ,
, ,当
,当 时,序号
时,序号 等于( )
等于( )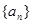 的前
的前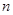 项和记为
项和记为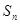 ,已知
,已知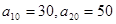 .
.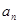 ;(2)若
;(2)若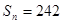 ,求
,求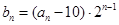 ,求数列
,求数列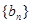 的前
的前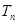 .
.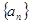 的前
的前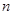 项和为
项和为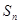 ,满足
,满足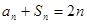 .
.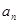 ;
;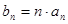 ,求数列
,求数列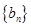 的前
的前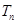 .
.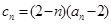 ,若对任意的正整数
,若对任意的正整数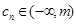 ,求实数
,求实数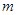 的取值范围.
的取值范围.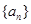 的前n项和为
的前n项和为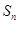 ,且
,且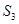 =6,
=6,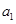 =4, 则公差d等于 ( )
=4, 则公差d等于 ( )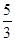
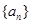 的前
的前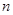 项和
项和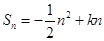 ,
,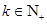 ,且
,且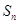 的最大值为8.
的最大值为8.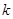 的值;
的值;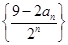 的前
的前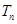 .
. 的前
的前 项和为
项和为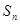 ,若
,若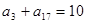 ,则
,则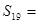 ( )
( )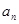 }中,
}中,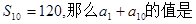 ( )
( )