题目内容
(10分)已知等比数列{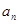 }的前n项和为
}的前n项和为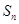 , 满足
, 满足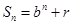 (
(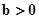
且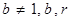 均为常数)
均为常数)
(1)求r的值; (4分)
(2)当b=2时,记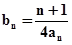
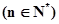 ,求数列
,求数列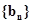 的前
的前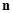 项的和
项的和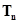 .(6分)
.(6分)
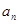 }的前n项和为
}的前n项和为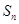 , 满足
, 满足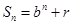 (
(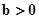
且
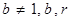 均为常数)
均为常数)(1)求r的值; (4分)
(2)当b=2时,记
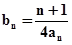
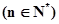 ,求数列
,求数列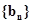 的前
的前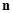 项的和
项的和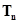 .(6分)
.(6分)(1)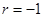 ;(2)证明:见解析。
;(2)证明:见解析。
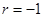 ;(2)证明:见解析。
;(2)证明:见解析。本试题主要是考查了等比数列的通项公式和前n项和的求解综合运用。
(1)因为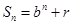 , 当
, 当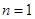 时,
时,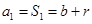 , 当
, 当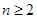 时,
时,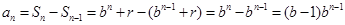 ,得到通项公式。
,得到通项公式。
(2)由(1)得等比数列{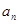 }的首项为
}的首项为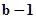 ,公比为
,公比为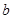 ,
, 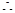
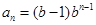 ,利用错位相减法得到结论。
,利用错位相减法得到结论。
解:(1)因为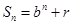 , 当
, 当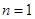 时,
时,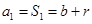 , -------1分
, -------1分
当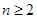 时,
时,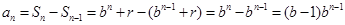 , ------3分
, ------3分
又因为{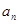 }为等比数列, 所以
}为等比数列, 所以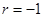 , -------------------4分
, -------------------4分
(2)证明:
由(1)得等比数列{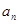 }的首项为
}的首项为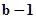 ,公比为
,公比为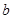 ,
, 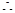
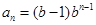 -------5分
-------5分
当b=2时,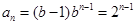 ,
, 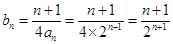 ------6分
------6分
设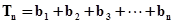 ,则
,则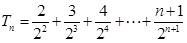
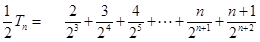 ----------------7分
----------------7分
两式相减, 得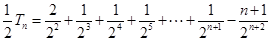 -------8分
-------8分
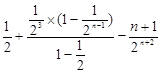
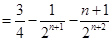 -------------9分
-------------9分
所以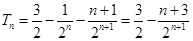 --------10分
--------10分
(1)因为
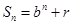 , 当
, 当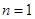 时,
时,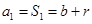 , 当
, 当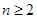 时,
时,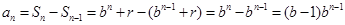 ,得到通项公式。
,得到通项公式。(2)由(1)得等比数列{
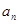 }的首项为
}的首项为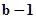 ,公比为
,公比为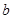 ,
, 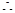
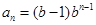 ,利用错位相减法得到结论。
,利用错位相减法得到结论。解:(1)因为
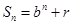 , 当
, 当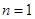 时,
时,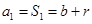 , -------1分
, -------1分当
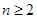 时,
时,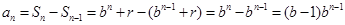 , ------3分
, ------3分又因为{
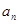 }为等比数列, 所以
}为等比数列, 所以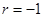 , -------------------4分
, -------------------4分(2)证明:
由(1)得等比数列{
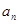 }的首项为
}的首项为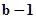 ,公比为
,公比为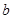 ,
, 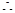
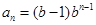 -------5分
-------5分当b=2时,
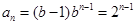 ,
, 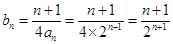 ------6分
------6分 设
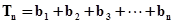 ,则
,则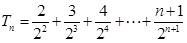
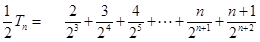 ----------------7分
----------------7分两式相减, 得
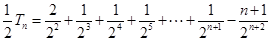 -------8分
-------8分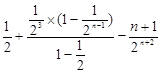
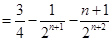 -------------9分
-------------9分 所以
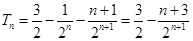 --------10分
--------10分
练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
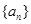 的前
的前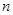 项和为
项和为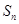 ,且满足
,且满足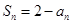 (
(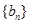 满足
满足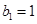 ,且
,且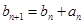 ,求数列
,求数列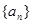 的前
的前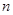 项和记为
项和记为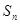 ,已知
,已知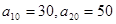 .
.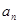 ;(2)若
;(2)若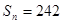 ,求
,求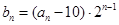 ,求数列
,求数列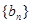 的前
的前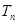 .
.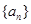 的前n项和为
的前n项和为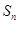 ,且
,且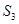 =6,
=6,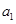 =4, 则公差d等于 ( )
=4, 则公差d等于 ( )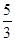
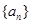 的前
的前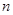 项和
项和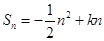 ,
,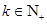 ,且
,且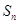 的最大值为8.
的最大值为8.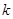 的值;
的值;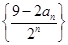 的前
的前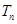 .
.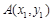 、
、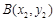 是函数
是函数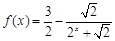 图象上任意两点,且
图象上任意两点,且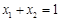 .
.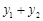 的值;
的值;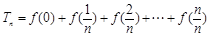 (其中
(其中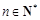 ),求
),求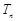 ;
;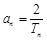 (
(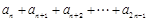 >
>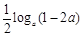 对任意的正整数n恒成立,求实数a的取值范围.
对任意的正整数n恒成立,求实数a的取值范围. 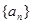 是等差数列,其前n项和为Sn,已知
是等差数列,其前n项和为Sn,已知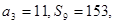
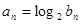 ,证明
,证明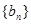 是等比数列,并求其前n项和Tn.
是等比数列,并求其前n项和Tn.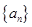 的前
的前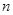 项和为
项和为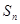 ,且
,且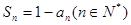 .
.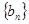 满足:
满足: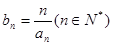 ,试求
,试求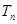 .
.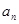 }中,
}中,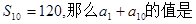 ( )
( )