题目内容
【题目】如图,设椭圆![]() (a>2)的离心率为
(a>2)的离心率为![]() ,斜率为k(k>0)的直线L过点E(0,1)且与椭圆交于C,D两点.
,斜率为k(k>0)的直线L过点E(0,1)且与椭圆交于C,D两点.
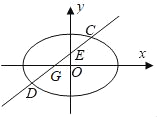
(Ⅰ)求椭圆的标准方程;
(Ⅱ)若直线l与x轴相交于点G,且![]() ,求k的值.
,求k的值.
【答案】(Ⅰ) ![]() (Ⅱ)
(Ⅱ) ![]()
【解析】
(Ⅰ)由椭圆的离心率公式和a,b,c的关系,解方程可得a,进而得到椭圆方程;
(Ⅱ)设直线l的方程为y=kx+1,求得G的坐标,设C(x1,y1),D(x2,y2),将直线方程代入椭圆方程,可得关于x的一元二次方程,运用根与系数关系和向量相等,可得关于k的方程,即可得到所求值.
(Ⅰ)由题意可得![]() ,
,
解得![]() =
=![]() ,
,
则椭圆方程为![]() ;
;
(Ⅱ)设直线l的方程为y=kx+1,可得G(﹣![]() ,0),
,0),
设C(x1,y1),D(x2,y2),
将直线方程代入椭圆方程![]() ,
,
可得(2+3k2)x2+6kx﹣9=0,
△=36k2+36(2+3k2)>0恒成立,
即有x1+x2=﹣![]() ,
,
则![]() ,
,![]() ,
,
由![]() ,可得x1+
,可得x1+![]() =0﹣x2,
=0﹣x2,
即有x1+x2+![]() =0,
=0,
即﹣![]() +
+![]() =0,
=0,
解得![]() =
=![]() (负的舍去).
(负的舍去).

【题目】“红灯停,绿灯行”,这是我们每个人都应该也必须遵守的交通规则.凑齐一拨人就过马路﹣﹣不看交通信号灯、随意穿行交叉路口的“中国式过马路”不仅不文明而且存在很大的交通安全隐患.一座城市是否存在“中国式过马路”是衡量这座城市文明程度的重要指标.某调查机构为了了解路人对“中国式过马路”的态度,从马路旁随机抽取30名路人进行了问卷调查,得到了如下列联表:
男性 | 女性 | 合计 | |
反感 | 10 | ||
不反感 | 8 | ||
合计 | 30 |
已知在这30人中随机抽取1人抽到反感“中国式过马路”的路人的概率是![]() .
.
(1)请将上面的列联表补充完整(在答题卷上直接填写结果,不需要写求解过程),并据此列联表数据判断是否有95%的把握认为反感“中国式过马路”与性别有关?
(2)若从这30人中的女性路人中随机抽取2人参加一项活动,记反感“中国式过马路”的人数为X,求X的分布列及其数学期望.
附:![]() ,其中n=a+b+c+d
,其中n=a+b+c+d
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |