题目内容
【题目】对于数集![]() ,其中
,其中![]() ,
, ![]() ,定义向量集
,定义向量集![]() .若对于任意
.若对于任意![]() ,使得
,使得![]() ,则称
,则称![]() 具有性质
具有性质![]() .例如
.例如![]() 具有性质
具有性质![]() .
.
(![]() )若
)若![]() ,且
,且![]() 具有性质
具有性质![]() ,求
,求![]() 的值.
的值.
(![]() )若
)若![]() 具有性质
具有性质![]() ,求证:
,求证: ![]() ,且当
,且当![]() 时,
时, ![]() .
.
(![]() )若
)若![]() 具有性质
具有性质![]() ,且
,且![]() ,
, ![]() (
(![]() 为常数),求有穷数列
为常数),求有穷数列![]() ,
, ![]() ,
, ![]() ,
, ![]() 的通项公式.
的通项公式.
【答案】(1)1;(2)见解析;(3)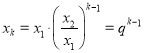 ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
【解析】试题分析:(Ⅰ)由于具有该性质,所以必有任意向量都存在垂直向量,可以求出![]() 值。
值。
(Ⅱ)取![]() ,设
,设![]() 满足
满足![]() ,可得
,可得![]() ,
, ![]() 、
、![]() 中之一为-1,另一为1,故1X,然后只要用反证法证明
中之一为-1,另一为1,故1X,然后只要用反证法证明![]() 之间不存在即可;
之间不存在即可;
(Ⅲ)可以利用后一项比前一项的比值建立数集,最终求出后一项与前一项比是定值,从而是等比数列.
试题解析:
(1)选取![]() ,Y中与
,Y中与![]() 垂直的元素必有形式
垂直的元素必有形式![]() .
.
所以x=2b,从而x=4.
(2)证明:取![]() .设
.设![]() 满足
满足![]() .
.
由![]() 得
得![]() ,所以
,所以![]() 、
、![]() 异号.
异号.
因为-1是X中唯一的负数,所以![]() 、
、![]() 中之一为-1
中之一为-1
故1X.
假设![]() ,其中
,其中![]() ,则
,则![]() .
.
选取![]() ,并设
,并设![]() 满足
满足![]() ,即
,即![]() ,
,
则![]() 、
、![]() 异号,从而
异号,从而![]() 、
、![]() 之中恰有一个为-1.
之中恰有一个为-1.
若![]() =-1,则
=-1,则![]() ,矛盾;
,矛盾;
若![]() =-1,则
=-1,则![]() ,矛盾.
,矛盾.
所以x1=1.
(3)设![]() ,
,![]() ,则
,则![]() 等价于
等价于![]() 。
。
记![]() ,则数集
,则数集![]() 具有性质
具有性质![]() 当且仅当数集
当且仅当数集![]() 关于原点对称。
关于原点对称。
注意到![]() 是
是![]() 中的唯一负数,
中的唯一负数,![]() 共有
共有![]() 个数,所以
个数,所以![]() 也只有
也只有![]() 个数。
个数。
由于,已有![]() 个数,对以下三角数阵,
个数,对以下三角数阵,
![]() ,
,![]()
![]() 。
。
注意到![]() ,所以
,所以![]() ,从而数列的通项为
,从而数列的通项为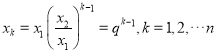 。
。

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目


