题目内容
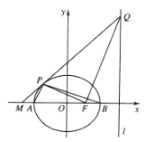
【题目】如图,在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的右准线方程
的右准线方程![]() ,离心率
,离心率![]() ,左、右顶点分别为A,B,右焦点为F,点P在椭圆上,且位于x轴上方.
,左、右顶点分别为A,B,右焦点为F,点P在椭圆上,且位于x轴上方.
(Ⅰ)设直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,求
,求![]() 的最小值;
的最小值;
(Ⅱ)点Q在右准线l上,且![]() ,直线
,直线![]() 交x负半轴于点M,若
交x负半轴于点M,若![]() ,求点P坐标.
,求点P坐标.
【答案】(Ⅰ)![]() .(Ⅱ)
.(Ⅱ)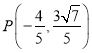
【解析】
(Ⅰ)利用离心率公式及准线方程,求出![]() 和
和![]() ,可得椭圆的方程,再利用斜率公式得出结论;
,可得椭圆的方程,再利用斜率公式得出结论;
(Ⅱ)设点![]() ,
,![]() ,利用
,利用![]() 和
和![]() 三点共线,结合斜率公式求出点P的坐标.
三点共线,结合斜率公式求出点P的坐标.
(Ⅰ)由题意可知,![]() ,
,
解得![]() ,
,
所以![]() ,
,
所以椭圆C的方程为![]() .
.
所以点![]() ,点
,点![]() ,
,
设点![]() ,
,![]()
则![]() .
.
因为![]() ,所以当
,所以当![]() 时,
时,![]() 取最小值,最小值为
取最小值,最小值为![]() .
.
(Ⅱ)由(Ⅰ)得![]() ,设点
,设点![]() ,
,![]()
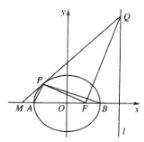
因为![]() ,
,
则![]() ,
,
所以点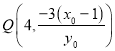 .
.
因为点![]() 三点共线,
三点共线,
所以![]() ,且点
,且点![]() ,
,
所以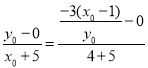 ,
,
所以![]() ,
,
又因为![]() ,所以
,所以![]() 。
。
所以![]() 或
或![]() ,
,
因为![]() ,所以
,所以![]() 舍去,
舍去,
所以![]() ,
,![]() (负值已舍去)
(负值已舍去)
所以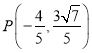 .
.

练习册系列答案
相关题目
【题目】某便利店每天以每件5元的价格购进若干鲜奶,然后以每件10元价格出售,如果当天卖不完,剩下的鲜奶作餐厨垃圾处理.便利店记录了100天这种鲜奶的日需求量![]() (单位:件)如表所示:
(单位:件)如表所示:
日需求量n(件) | 140 | 150 | 160 | 170 | 180 | 190 | 200 |
频数 | 10 | 20 | 16 | 16 | 15 | 12 | 11 |
以100天记录的各需求量的频率作为各需求量发生的概率.
(1)若便利店一天购进160件这种鲜奶,X表示当天的利润(单位:元),求X的分布列与数学期望及方差;
(2)若便利店一天购进160件或170件这种鲜奶,仅从获得利润大的角度考虑,你认为应购进160件还是170件?请说明理由.