题目内容
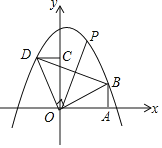
【题目】如图所示,Rt△AOB的直角边OA在x轴上,OA=2,AB=1,将Rt△AOB绕点O逆时针旋转90°得到![]() ,抛物线
,抛物线![]() 经过B、D两点.
经过B、D两点.
(1)求二次函数的解析式;
(2)连接BD,点P是抛物线上一点,直线OP把△BOD的周长分成相等的两部分,求点P的坐标.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】
(1)由旋转性质可得CD=AB=1,OA=OC=2,从而得到点B,D的坐标,代入解析式即可得出答案;
(2)由直线OP把![]() 的周长分成相等的两部分,且OB=OD,知DQ=BQ,即点Q为BD的中点,从而得到点Q的坐标,求得直线OP解析式,代入抛物线解析式可得点P的坐标.
的周长分成相等的两部分,且OB=OD,知DQ=BQ,即点Q为BD的中点,从而得到点Q的坐标,求得直线OP解析式,代入抛物线解析式可得点P的坐标.
(1)∵Rt△AOB绕点O逆时针旋转90°得到Rt△COD,
∴CD=AB=1,OA=OC=2,则点B(2,1),D(﹣1,2),代入解析式,
得 ,解得
,解得![]() ,
,
∴二次函数的解析式为y=﹣![]() x2+
x2+![]() x+
x+![]() .
.
(2)如图:

∵OA=2,AB=1,∴B(2,1).
∵直线OP把△BOD的周长分成相等的两部分,且OB=OD,
∴DQ=BQ,即点Q为BD的中点,D(﹣1,2),
∴点Q坐标为(![]() ,
,![]() ).
).
设直线OP解析式为y=kx,
将点Q坐标代入,得![]() k=
k=![]() ,解得k=3,
,解得k=3,
∴直线OP的解析式为y=3x,
代入y=﹣![]() x2+
x2+![]() x+
x+![]() ,得﹣
,得﹣![]() x2+
x2+![]() x+
x+![]() =3x,
=3x,
解得x=1或x=﹣4.
当x=1时,y=3;当x=﹣4时,y=﹣12.
∴点P坐标为(1,3)或(﹣4,﹣12).

练习册系列答案
相关题目


