题目内容
15.已知函数f(x)=lnx+mx(m>0),其中e=2.71828…为自然对数的底数.(1)若函数f(x)的图象经过点($\frac{1}{e}$,0),求m的值;
(2)试判断函数f(x)的单调性,并予以说明;
(3)试确定函数f(x)的零点个数.
分析 (1)代入点的坐标秒即可求出m的值,
(2)利用定义证明即可;
(3)需要分类讨论,当m∈(0,e)时,根据函数零点定理,以及函数的单调性,
当m=e时,当m∈(e,+∞)时,f(x)在定义域上单调递增,得到结论,
当m∈(e,+∞)时,设x0=m-e>0根据函数零点定理,以及函数的单调性,即可得到结论或构造函数,设$g(x)={e^x}-\frac{m}{x}(m>e)$,根据根据函数零点定理得到结论.
解答 解:(1)因为函数f(x)的图象经过点$(\frac{1}{e},0)$,
所以 $0=ln\frac{1}{e}+\frac{m}{e}$,
所以 m=e;
(2)因为函数f(x)的定义域为(0,+∞),设0<x1<x2,
所以 f(x1)=lnx1+mx1,f(x2)=lnx2+mx2,
所以 $f({x_1})-f({x_2})=ln{x_1}-ln{x_2}+m({x_1}-{x_2})=ln\frac{x_1}{x_2}+m({x_1}-{x_2})$,
因为0<x1<x2,m>0,所以 $\frac{x_1}{x_2}<1$,所以$ln\frac{x_1}{x_2}+m({x_1}-{x_2})<0$,
所以 f(x1)-f(x2)<0,即f(x1)<f(x2),
所以 f(x)在定义域上单调递增.
(3)函数f(x)的零点只有一个
①当m∈(0,e)时,f(1)=ln1+m=m>0$f({e^{-1}})=ln{e^{-1}}+m{e^{-1}}=-1+\frac{m}{e}=\frac{m-e}{e}<0$,
且函数f(x)在$[\frac{1}{e},1]$上的图象是连续不间断曲线,
所以由零点定理可得 函数f(x)在(e-1,1)上存在一个零点,
又由(2)得f(x)在定义域上单调递增,所以函数f(x)的零点只有一个.
②当m=e时,$f(\frac{1}{e})=-1+\frac{e}{e}=0$,又由(2)得f(x)在定义域上单调递增,
所以函数f(x)的零点只有一个.
方法一:
③当m∈(e,+∞)时,设x0=m-e>0
则f(1)=ln1+m=m>0$f({e^{-{x_0}-2}})=ln{e^{-{x_0}-2}}+m{e^{-{x_0}-2}}=-{x_0}-2+\frac{{{x_0}+e}}{{{e^{{x_0}+2}}}}=-{x_0}-2+\frac{x_0}{{{e^{{x_0}+2}}}}+\frac{1}{{{e^{{x_0}+1}}}}$,
因为x0>0,所以$\frac{1}{{{e^{{x_0}+1}}}}<1,\frac{x_0}{{{e^{{x_0}+2}}}}<1$,
所以 $-{x_0}-2+\frac{x_0}{{{e^{{x_0}+2}}}}+\frac{1}{{{e^{{x_0}+1}}}}<-{x_0}-2+2=-{x_0}<0$,即$f({e^{-{x_0}-2}})<0$,
且函数f(x)在$({e^{-{x_0}-2}},1)$上的图象是连续不间断曲线
所以由零点定理可得 函数f(x)在$({e^{-{x_0}-2}},1)$上存在一个零点,
又由(2)得f(x)在定义域上单调递增,所以函数f(x)的零点只有一个.
方法二:
③当m∈(e,+∞)时,设$g(x)={e^x}-\frac{m}{x}(m>e)$
则$g(1)=e-m<0,g(m)={e^m}-\frac{m}{m}={e^m}-1>0$,
且函数g(x)在[1,m]上的图象是连续不间断曲线
所以存在x0∈(1,m),使得g(x0)=0,即$m={x_0}{e^{x_0}}$,
从而有$f({e^{-{x_0}}})=-{x_0}+m{e^{-{x_0}}}=-{x_0}+{x_0}=0$,
且函数f(x)在(0,+∞)上的图象是连续不间断曲线
又由(2)得f(x)在定义域上单调递增,
所以当m∈(e,+∞)时,函数f(x)的零点只有一个.
点评 本题考查了函数零点存在定理和函数的单调性,培养可分类讨论的能力,转化能力,运算能力,属于中档题.

| A. | 相同的离心率 | B. | 相同的焦点 | C. | 相同的顶点 | D. | 相同的长、短轴 |
| A. | $\frac{x^2}{9}-\frac{y^2}{16}=1$ | B. | $\frac{x^2}{169}-\frac{y^2}{144}=1$ | C. | $\frac{x^2}{169}-\frac{y^2}{25}=1$ | D. | $\frac{x^2}{16}-\frac{y^2}{9}=1$ |
| A. | $\frac{1}{2}$ | B. | $\sqrt{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | 2 |
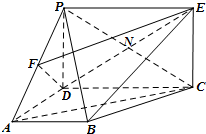 如图,PD垂直于梯形ABCD所在的平面,∠ADC=∠BAD=90°.F为PA中点,PD=$\sqrt{2}$,AB=AD=$\frac{1}{2}$CD=1.四边形PDCE为矩形,线段PC交DE于点N.
如图,PD垂直于梯形ABCD所在的平面,∠ADC=∠BAD=90°.F为PA中点,PD=$\sqrt{2}$,AB=AD=$\frac{1}{2}$CD=1.四边形PDCE为矩形,线段PC交DE于点N.