题目内容
(本题满分14分)已知椭圆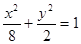 经过点
经过点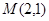 ,
,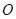 为坐标原点,平行于
为坐标原点,平行于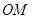 的直线
的直线 在
在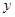 轴上的截距为
轴上的截距为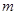
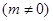 .
.
(1)当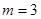 时,判断直线
时,判断直线 与椭圆的位置关系(写出结论,不需证明);
与椭圆的位置关系(写出结论,不需证明);
(2)当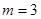 时,
时,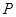 为椭圆上的动点,求点
为椭圆上的动点,求点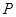 到直线
到直线  距离的最小值;
距离的最小值;
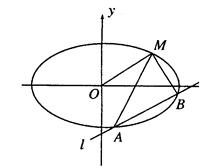
(3)如图,当 交椭圆于
交椭圆于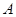 、
、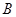 两个不同点时,求证:直线
两个不同点时,求证:直线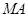 、
、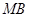 与
与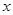 轴始终围成一个等腰三角形.
轴始终围成一个等腰三角形.
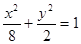 经过点
经过点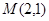 ,
,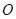 为坐标原点,平行于
为坐标原点,平行于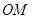 的直线
的直线 在
在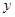 轴上的截距为
轴上的截距为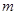
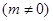 .
.(1)当
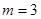 时,判断直线
时,判断直线 与椭圆的位置关系(写出结论,不需证明);
与椭圆的位置关系(写出结论,不需证明);(2)当
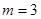 时,
时,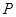 为椭圆上的动点,求点
为椭圆上的动点,求点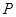 到直线
到直线  距离的最小值;
距离的最小值;(3)如图,当
 交椭圆于
交椭圆于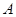 、
、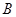 两个不同点时,求证:直线
两个不同点时,求证:直线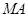 、
、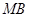 与
与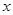 轴始终围成一个等腰三角形.
轴始终围成一个等腰三角形.
解:(1)当 时,直线
时,直线 与椭圆相离. ……2分
与椭圆相离. ……2分

(2)可知直线 的斜率为
的斜率为
设直线 与直线
与直线 平行,且直线
平行,且直线 与椭圆相切,
与椭圆相切,
设直线 的方程为
的方程为 --------------------------------- 3分
--------------------------------- 3分
联立 ,得
,得 --------------------------------- 4分
--------------------------------- 4分
 ,解得
,解得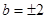 --------------------------------- 5分
--------------------------------- 5分
 直线
直线 的方程为
的方程为 .
.
所求点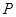 到直线
到直线 的最小距离等于直线
的最小距离等于直线 到直线
到直线 的距离
的距离
 . ------------------------------ 7分
. ------------------------------ 7分
(3)由
若点 与
与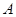 关于x轴对称,则
关于x轴对称,则 ,
,
此时直线 :
: .
.
由上题知,直线 与椭圆相切,不合题意.
与椭圆相切,不合题意.
故设直线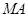 、
、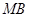 的斜率分别为
的斜率分别为 ,
, ,
,
只需证明 +
+ 即可.
即可.
设 ,
,
 ,
, -----------------------------9分
-----------------------------9分
而 ----------- 10分
----------- 10分
 ----------- 12分
----------- 12分


∴ +
+
直线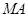 、
、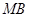 与
与 轴始终围成一个等腰三角形 ---------------------------------------14分
轴始终围成一个等腰三角形 ---------------------------------------14分
 时,直线
时,直线 与椭圆相离. ……2分
与椭圆相离. ……2分
(2)可知直线
 的斜率为
的斜率为
设直线
 与直线
与直线 平行,且直线
平行,且直线 与椭圆相切,
与椭圆相切,设直线
 的方程为
的方程为 --------------------------------- 3分
--------------------------------- 3分联立
 ,得
,得 --------------------------------- 4分
--------------------------------- 4分 ,解得
,解得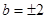 --------------------------------- 5分
--------------------------------- 5分 直线
直线 的方程为
的方程为 .
.所求点
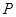 到直线
到直线 的最小距离等于直线
的最小距离等于直线 到直线
到直线 的距离
的距离  . ------------------------------ 7分
. ------------------------------ 7分(3)由

若点
 与
与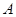 关于x轴对称,则
关于x轴对称,则 ,
,此时直线
 :
: .
.由上题知,直线
 与椭圆相切,不合题意.
与椭圆相切,不合题意.故设直线
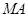 、
、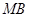 的斜率分别为
的斜率分别为 ,
, ,
,只需证明
 +
+ 即可.
即可.设
 ,
,
 ,
, -----------------------------9分
-----------------------------9分而
 ----------- 10分
----------- 10分
 ----------- 12分
----------- 12分

∴
 +
+
直线
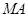 、
、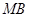 与
与 轴始终围成一个等腰三角形 ---------------------------------------14分
轴始终围成一个等腰三角形 ---------------------------------------14分略

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
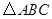 的顶点
的顶点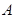 ,
,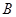 在椭圆
在椭圆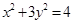 上,
上,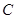 在直线
在直线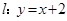 上,且
上,且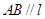 .
.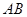 边通过坐标原点
边通过坐标原点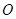 时,求
时,求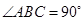 ,且斜边
,且斜边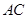 的长最大时,求
的长最大时,求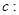
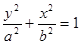 (a>b>0)的离心率
(a>b>0)的离心率
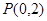 为
为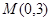 作直线
作直线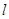 与椭圆
与椭圆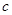 相交于
相交于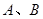 点,若以
点,若以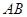 为直径的圆经原点
为直径的圆经原点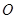 ,求直线
,求直线
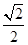


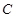 的方程为
的方程为 ,点
,点 和点
和点 (其中
(其中 和
和 均为正数)是双曲线
均为正数)是双曲线 满足
满足 (其中
(其中 ).
). 的解析式表示
的解析式表示 ;
; (
( 为坐标原点)面积的取值范围.
为坐标原点)面积的取值范围.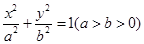 的左、右焦点分别为
的左、右焦点分别为 ,点
,点 满足
满足 .
. ;
;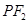 与椭圆相交于A,B两点.若直线
与椭圆相交于A,B两点.若直线 相交于M,N两点,且|MN|=
相交于M,N两点,且|MN|= |AB|,求椭圆的方程.
|AB|,求椭圆的方程. 的离心率为( )
的离心率为( )
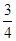


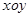 中,向量
中,向量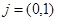 ,△OFP的面积为
,△OFP的面积为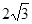 ,且
,且
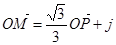 。
。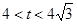 ,求向量
,求向量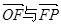 的夹角
的夹角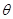 的取值范围;
的取值范围;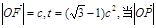 取最小值时,求椭圆的方程。
取最小值时,求椭圆的方程。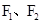 分别是椭圆
分别是椭圆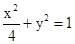 的左右焦点,若P是该椭圆上的一个动点则
的左右焦点,若P是该椭圆上的一个动点则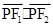 最大值和最小值分别是 ( )
最大值和最小值分别是 ( )


