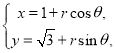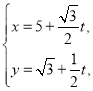题目内容
【题目】已知椭圆![]() ,过
,过![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,且与
两点,且与![]() 轴相交于
轴相交于![]() 点.
点.
(1)若![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)设![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,证明:直线
,证明:直线![]() 过
过![]() 轴上的定点.
轴上的定点.
【答案】(1)![]() 或
或![]() ;(2)见解析
;(2)见解析
【解析】
(1)由已知条件利用点斜式设出直线![]() 的方程,则可表示出点
的方程,则可表示出点![]() 的坐标,再由
的坐标,再由![]() 的关系表示出点
的关系表示出点![]() 的坐标,而点
的坐标,而点![]() 在椭圆上,将其坐标代入椭圆方程中可求出直线的斜率;
在椭圆上,将其坐标代入椭圆方程中可求出直线的斜率;
(2)设出![]() 两点的坐标,则点
两点的坐标,则点![]() 的坐标可以表示出,然后直线
的坐标可以表示出,然后直线![]() 的方程与椭圆方程联立成方程,消元后得到关于
的方程与椭圆方程联立成方程,消元后得到关于![]() 的一元二次方程,再利用根与系数的关系,再结合直线
的一元二次方程,再利用根与系数的关系,再结合直线![]() 的方程,化简可得结果.
的方程,化简可得结果.
(1)由条件可知直线![]() 的斜率存在,则
的斜率存在,则
可设直线![]() 的方程为
的方程为![]() ,则
,则![]() ,
,
由![]() ,有
,有![]() ,
,
所以![]() ,
,
由![]() 在椭圆
在椭圆![]() 上,则
上,则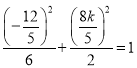 ,解得
,解得![]() ,此时
,此时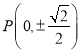 在椭圆
在椭圆![]() 内部,所以满足直线
内部,所以满足直线![]() 与椭圆相交,
与椭圆相交,
故所求直线![]() 方程为
方程为![]() 或
或![]() .
.
(也可联立直线![]() 与椭圆方程,由
与椭圆方程,由![]() 验证)
验证)
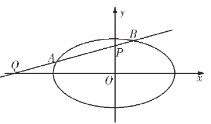
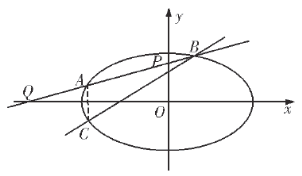
(2)设![]() ,则
,则![]() ,
,
直线![]() 的方程为
的方程为![]() .
.
由![]() 得
得![]() ,
,
由![]() ,
,
解得![]() ,
,
![]() ,
,
当![]() 时,
时,![]()
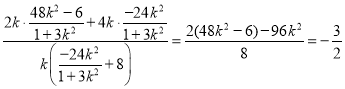 ,
,
故直线![]() 恒过定点
恒过定点![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】微信是腾讯公司推出的一种手机通讯软件,它支持发送语音、短信、视频、图片和文字,一经推出便风靡全国,甚至涌现出一批在微信的朋友圈内销售商品的人(被称为微商).为了调查每天微信用户使用微信的时间,某经销化妆品的微商在一广场随机采访140位市民进行调查,其中每天玩微信超过6小时的用户称为“微信控”,否则称其为“非微信控”, 调查结果统计如下:
微信控 | 非微信控 | 合计 | |
女性 | 60 | ||
男性 | 30 | ||
合计 | 70 | 140 |
(1)根据以上数据,把表格中的数据填写完整;
(2)利用(1)完成的表格数据回答下列问题:
①是否在犯错误的概率不超过0.001的前提下认为“微信控”与“性别”有关;
②已知在被调查的女性“微信控”市民中有5位退休老人,其中2位是教师,现从这5位退休老人中随机抽取2人,求至少有1位老师的概率.
附表:![]() 其中
其中![]()
P(K2≥k) | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |