题目内容
13.复数z满足(z-2i)(1+i)=|1+$\sqrt{3}$i|(i为虚数单位),则复数z=1+i.分析 求出复数的模,然后利用复数的乘除运算法则化简求解即可.
解答 解:复数z满足(z-2i)(1+i)=|1+$\sqrt{3}$i|=2,
所以z=$\frac{2}{1+i}+2i$=$\frac{2-2i}{(1+i)(1-i)}+2i$=1+i.
故答案为:1+i.
点评 本题考查复数的模的求法,复数的乘除运算法则的应用,考查计算能力.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
8.复数z=$\frac{1-2i}{3+4i}$(i为虚数单位)的实部为( )
| A. | -$\frac{2}{5}$ | B. | -1 | C. | -$\frac{1}{5}$ | D. | $\frac{11}{25}$ |
18.若复数Z=2cosθ+isinθ (θ∈R),则z$\overline{z}$的最大值为( )
| A. | 1 | B. | 2 | C. | 4 | D. | $\sqrt{5}$ |
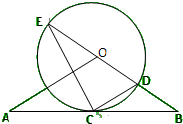 (如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,⊙O交直线OB于E,D,连接EC,CD.
(如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,⊙O交直线OB于E,D,连接EC,CD. 如图,在圆内接四边形ABCD中,AB∥DC,过点A作圆的切线与CB的延长线交于点E.若AB=AD=BC=5,AE=6,则DC=$\frac{25}{4}$.
如图,在圆内接四边形ABCD中,AB∥DC,过点A作圆的切线与CB的延长线交于点E.若AB=AD=BC=5,AE=6,则DC=$\frac{25}{4}$. 已知函数f1(x)=x2,f2(x)=x-1,f3(x)=x${\;}^{\frac{1}{2}}$,如果执行如图的程序框图,那么输出S的值为$\frac{1}{2011}$.
已知函数f1(x)=x2,f2(x)=x-1,f3(x)=x${\;}^{\frac{1}{2}}$,如果执行如图的程序框图,那么输出S的值为$\frac{1}{2011}$.