题目内容
【题目】已知函数![]() ,若方程
,若方程![]() 有五个不同的实数根,则
有五个不同的实数根,则![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
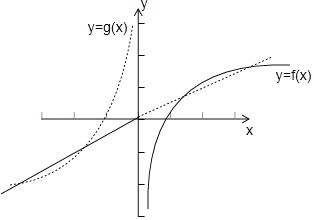
由方程的解与函数图象的交点问题得:方程f(﹣x)=﹣f(x)有五个不同的实数根等价于y=f(x)的图象与y=g(x)的图象有5个交点,作图可知,只需y=ax与曲线y=lnx在第一象限由两个交点即可,利用导数求切线方程得:设过原点的直线与y=lnx切于点P(x0,y0),得lnx0=1,即f′(e)![]() ,即过原点的直线与y=lnx相切的直线方程为y
,即过原点的直线与y=lnx相切的直线方程为y![]() x,即所求a的取值范围为0
x,即所求a的取值范围为0![]() ,得解.
,得解.
设g(x)=﹣f(﹣x),则y=g(x)的图象与y=f(x)的图象关于原点对称,
方程f(﹣x)=﹣f(x)有五个不同的实数根等价于函数y=f(x)的图象与y=g(x)的图象有5个交点,
由图可知,只需y=ax与曲线y=lnx在第一象限有两个交点即可,
设过原点的直线与y=lnx切于点P(x0,y0),
由f′(x)![]() ,
,
则y=lnx的切线为y﹣lnx0![]() (x﹣x0),
(x﹣x0),
又此直线过点(0,0),
所以lnx0=1,
所以x0=e,
即f′(e)![]() ,
,
即过原点的直线与y=lnx相切的直线方程为y![]() x,
x,
即所求a的取值范围为0![]() ,
,
故选:B.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目