题目内容
【题目】给出下面四个命题：
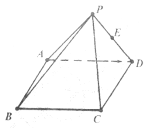
①“直线
平面
内所有直线”的充要条件是“平面”；
②“直线
直线
”的充要条件是“
平行于所在的平面”；
③“直线，为异面直线”的充分不必要条件是“直线，不相交”；
④“平面
平面
”的必要不充分条件是“内存在不共线三点到的距离相等”.
其中正确命题的序号是____________________
【答案】①④
【解析】
利用直线与直线、平面与平面间的位置关系及性质判断前后两个条件的推出关系，利用充要条件的定义得结论．
解：对于①直线与平面垂直的定义是直线与平面内的所有直线垂直，故①正确；
对于②，
平行于
所在的平面
或与异面，故②错；
对于③，直线、不相交
直线，异面或平行，故③错；
对于④，平面
平面
内存在不共线三点到
的距离相等；
内存在不共线三点到的距离相等平面平面或相交，故④正确
故答案为：①④
【题目】某企业购买某种仪器，在仪器使用期间可能出现故障，需要请销售仪器的企业派工程师进行维修，因为考虑到人力、成本等多方面的原因，销售仪器的企业提供以下购买仪器维修服务的条件：在购买仪器时，可以直接购买仪器维修服务，维修一次1000元；在仪器使用期间，如果维修服务次数不够再次购买，则需要每次1500元..现需决策在购买仪器的同时购买几次仪器维修服务，为此搜集并整理了500台这种机器在使用期内需要维修的次数，得到如下表格：
维修次数 | 5 | 6 | 7 | 8 | 9 |
频数（台） | 50 | 100 | 150 | 100 | 100 |
记
表示一台仪器使用期内维修的次数，
表示一台仪器使用期内维修所需要的费用，
表示购买仪器的同时购买的维修服务的次数.
（1）若
，求与的函数关系式；
（2）以这500台仪器使用期内维修次数的频率代替一台仪器维修次数发生的概率，求
的概率.
（3）假设购买这500台仪器的同时每台都购买7次维修服务，或每台都购买8次维修服务，请分别计算这500台仪器在购买维修服务所需要费用的平均数，以此为决策依据，判断购买7次还是8次维修服务？
