Question

【题目】已知某几何体的三视图如图所示（单位：cm），则此几何体的体积为 ， 表面积为 ．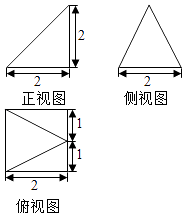

Answer 1

【答案】 ；
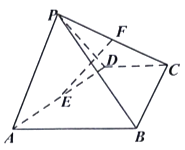
【解析】解：根据三视图可知几何体是一个四棱锥，

底面是一个边长为2的正方形，PE⊥面ABCD，且PE=2，

其中E、F分别是BC、AD的中点，连结EF、PA，

∴几何体的体积V= = ，

在△PEB中，PB= = ，同理可得PC= ，

∵PE⊥面ABCD，∴PE⊥CD，

∵CD⊥BC，BC∩PE=E，∴CD⊥面PBC，则CD⊥PC，

在△PCD中，PD= = =3，

同理可得PA=3，则PF⊥AD，

在△PDF中，PF= = = ，

∴此几何体的表面积S=2×2+ + +

=

所以答案是： ； ．

【考点精析】本题主要考查了由三视图求面积、体积的相关知识点，需要掌握求体积的关键是求出底面积和高；求全面积的关键是求出各个侧面的面积才能正确解答此题．